小梅在物理老师的指导下,利用一个重物、细线、若干钩码及杠杆来探究“杠杆平衡的条件”。
(1)实验前,为便于力臂的测量,她应通过调节杠杆两端的 使杠杆在 位置平衡。
(2)实验时,小梅决定先保持阻力 和阻力臂 不变,探究“杠杆平衡时,动力臂和动力之间的关系”。
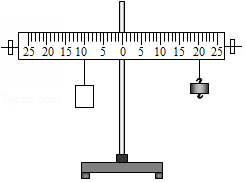
于是,她用细线将重物固定到杠杆左侧某一位置处;然后在杠杆右侧用细线悬挂一个钩码,移动其悬挂的位置,使杠杆重新在水平位置平衡,如图所示,将动力 和动力臂 记录下来。
接下来,她要改变 并移动其悬挂的位置,多次重复前面的实验,并把相应的数据记录下来。
(3)小梅通过实验得到的实验数据如表1所示。
表一 保持阻力 和阻力臂 不变,探究杠杆平衡时动力臂和动力之间的关系
实验序号 |
动力 |
动力臂 |
1 |
0.5 |
0.20 |
2 |
1.0 |
0.10 |
3 |
1.5 |
0.07 |
4 |
2.0 |
0.05 |
5 |
2.5 |
0.04 |
分析表1中的数据,小梅得出的结论是:保持阻力和阻力臂不变,杠杆平衡时,动力臂 跟动力 成 关系。
(4)在前面实验的基础上,小梅进一步猜想:在更普遍的情况下,杠杆平衡时可能满足“动力 动力臂 阻力臂 阻力臂 ”
为了验证小梅的这个猜想,小丽通过实验得到的实验数据如表2所示
表2 探究杠杆平衡时,动力 、动力臂 和阻力 、阻力臂 之间的关系
实验次数 |
动力 |
动力臂 |
阻力 |
阻力臂 |
1 |
1.0 |
0.10 |
1.0 |
0.10 |
2 |
1.5 |
0.08 |
1.5 |
0.08 |
3 |
2.0 |
0.07 |
2.0 |
0.07 |
小梅认为,表2中小丽的实验数据缺乏普遍性,用来验证她的猜想不够充分,于是对小丽的实验和收集数据提出了具体的建议。
小梅的建议是:小丽还要在 的情况下进行实验和收集数据。
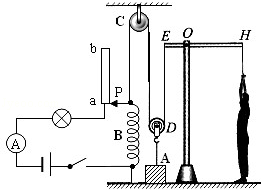
一绝缘细绳的一端与可绕O点转动的轻质杠杆的E端相连,另一端绕过动滑轮D、定滑轮C,与滑动变阻器的滑片P相连;B为一可导电的轻质弹簧,如图所示接入电路中,一端通过绝缘绳固定在地面上,另一端与滑片P相连;一人站在地面上拉住与杠杆H端相连的细绳.已知电源电压为8V,灯泡标有"6V 3W"字样,人的质量为50kg,人与地面的接触面积为50cm 2,EO:HO=2:5.人对绳子拉力最小时,电流表示数为I1,且滑片刚好位于滑动变阻器的a端;人对绳子拉力最大时,电流表示数为I 2,且I 1:I 2=2:1,滑动变阻器的阻值与弹簧所受拉力的关系如下表所示:
| R(Ω) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
… |
| F(N) |
0.5 |
50.5 |
100.5 |
150.5 |
200.5 |
250.5 |
300.5 |
350.5 |
… |
不计杠杆、弹簧、滑片、细绳的重力,不计摩擦,不计弹簧电阻.整套装置始终处于平衡状态,物体A始终不离开地面.灯泡电阻不变,且不会被烧坏.g=10N/kg.求:
(1)人的拉力最大时,滑动变阻器接入电路的阻值是多少?
(2)物体A的质量是多少?
(3)人的拉力最大时,人对地面的压强是多少?
(4)当灯泡正常发光时,物体A对地面的压力是多少?
如图是一种自动测定油箱内油面高度的装置,R是滑动变阻器,它的金属滑片是杠杆的一端,且受定位挡板限制只能在电阻上滑动.当油面在A处时,滑动变阻器的滑片恰好在最下端;当油面在B处时,滑动变阻器的滑片在最上端.从油量表(由电流表改装而成)指针所指的刻度,可以知道油箱内油面的高度.现已知油的密度ρ=0.8×103kg/m3,电源电压是6V,定值电阻R′的阻值是12Ω.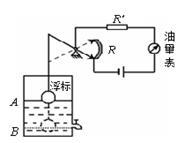
(1)若浮标有2×10-4m3的体积浸入油中,则油对它的浮力是多大?(g取10N/kg)提示:F浮=ρ油gV排
(2)当油面处在A处时,电流表示数为多少?
(3)已知电流增大时,电流表指针向右偏转,则_____.
| A.油面下降时,电流表指针向右偏转 |
| B.油量表零刻度线一定与电流表原零刻度线相重合 |
| C.油量表的刻度值从左往右是逐渐增大的 |
| D.油箱内的油越少,流过电流表的电流越大 |
如图,小明用一轻质杠杆自制简易密度秤的过程中,在A端的空桶内分别注入密度已知的不同液体,改变物体M悬挂点B的位置,当杠杆在水平位置平衡时,在M悬挂点处标出相应液体的密度值。下列关于密度秤制作的说法中,错误的是( )

| A.每次倒入空桶的液体体积相同 |
| B.秤的刻度值向右越来越大 |
| C.悬点O适当右移,秤的量程会增大 |
| D.增大M的质量,秤的量程会增大 |
如图,小明用一轻质杠杆自制简易密度秤的过程中,在A端的空桶内分别注入密度已知的不同液体,改变物体M悬挂点B的位置,当杠杆在水平位置平衡时,在M悬挂点处标出相应液体的密度值。下列关于密度秤制作的说法中,错误的是( )
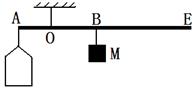
| A.每次倒入空桶的液体体积相同 |
| B.秤的刻度值向右越来越大 |
| C.悬点O适当右移,秤的量程会增大 |
| D.增大M的质量,秤的量程会增大 |
如图所示,有一轻质木板(质量忽略不计),左端可绕O点转动,长为L,右端放一重为G的物块,并用一竖直向上的力F拉着.当物块向左匀速滑动时,木板始终在水平位置保持静止,则下列表示拉力F与物块运动时间t的关系图中,正确的是( )

A.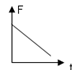 B.
B. C.
C.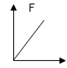 D
D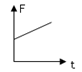
如图所示,平直的薄板AB长1m,重力忽略不计,B端用细绳悬于天花板上,绳与水平方向夹角为30°,薄板始终保持水平.一辆重20N、功率为1W的电动小车,从A端以0.2m/s的速度向右匀速行驶4s,细绳恰好被拉断,求: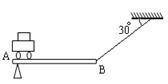
(1)小车行驶过程中牵引力做的功;
(2)小车运动时受到的阻力;
(3)细绳恰好被拉断时能承受的最大拉力.
某科技小组进行科技小游戏,一位同学站在墙边,身体竖直靠紧墙壁,将外侧的脚抬起,如图所示,则这位同学( )
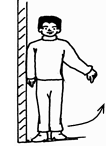
| A.仍能站住,因为仍然有一只脚着地和墙壁依靠 |
| B.倾倒,因为外侧的脚抬起后,人就会以另一只脚为支点转动,把人想象成一个杠杆模型,这个杠杆不会在如图所示的位置平衡的。 |
| C.都有可能,因为个人的平衡能力不一样 |
| D.人必须把外侧的手同时侧举,才有可能与外侧抬起的脚相平衡。 |
如图所示,O为杠杆的支点,在杠杆的右端B点挂一重物。MN是以A为圆心的弧形导轨,绳的一端系在杠杆的A点,另一端E可以在弧形导轨上自由滑动。当绳的E端从导轨的一端N点向另一端M点滑动的过程中,杠杆始终水平,绳AE对杠杆拉力的变化情况:( )

| A.先变小,后变大 | B.先变大,后变小 |
| C.一直变小 | D.一直变大 |
如图所示,用竖直向上的力F匀速拉动较长的杠杆,使重为10N的物体缓慢升高0.1m,拉力大小为8N,拉力移动的距离为0.25m。人做的有用功为_ J,该杠杆的机械效率为 ,此杠杆属于 (选填“省力”、“费力”或“等臂”)杠杆。
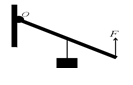
如图所示,可绕O点转动的轻质杠杆,在D点挂一个重为G的物体M.用一把弹簧测力计依次在A、B、C三点沿与圆O相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为F1、F2、F3,它们的大小关系是( )

A.F1<F2<F3<G B.F1>F2>F3>G
C. F1>F2=F3=G D.F1=F2=F3=G
如图所示,用固定在墙上的三角支架ABC放置空调室外机.如果A处螺钉松脱,则支架会绕 (选填“A”、“ B”或“C”)点倾翻.已知AB长40cm,AC长30cm,室外机的重力为300N,正好处在AB中点处,则A处螺钉的水平拉力为 N(支架重力不计).为了安全,室外机应尽量 (选填“靠近”或“远离”)墙壁.

如图所示,杠杆MN可绕O点转动,A、B、C、D是四个供人娱乐的吊环、B环到O点的距离为D环O点距离的一半,父子俩在吊环上做游戏,质量为40kg的儿子吊在B环上,父亲站在地面上抓着D环.(g=10N/kg)求: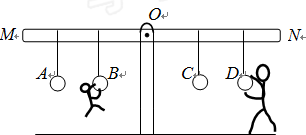
⑴ 若不计杠杆和吊环的重以及转轴间的摩擦,为使杠杆在水平位置平衡,父亲要用多大的力拉吊环D?
⑵ 若父亲实际使用竖直向下的拉力为250N,在4s内将儿子匀速拉高0.5m,父亲要做多少功?做功的功率多大?
⑶ 父亲提升儿子的过程中,该器材的机械效率为多少?
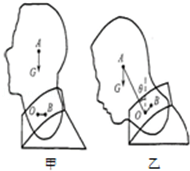
“低头族”长时间低头看手机,会引起颈部肌肉损伤.当头颅为竖直状态时,颈部肌肉的拉力为零,当头颅低下时,颈部肌肉会产生一定的拉力.为了研究颈部肌肉的拉力与低头角度大小的关系,我们可以建立一个头颅模型来模拟实验,如图甲所示.把人的颈椎简化成一个支点O,用1kg的头颅模型在重力作用下绕着这个支点O转动,A点为头颅模型的重心,B点为肌肉拉力作用点.将细线的一端固定在B点,用弹簧测力计拉着细线模拟测量肌肉的拉力,头颅模型在转动过程中,细线拉力的方向始终垂直于OB,如图乙所示.让头颅模型从竖直状态开始转动,通过实验记录出低头角度θ及细线拉力F的数据.如表:
| 低头角度θ/° |
0 |
15 |
30 |
45 |
60 |
| 细线拉力F/N |
0 |
7.3 |
14.0 |
20.2 |
25.0 |
(1)头颅模型质量为1kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N;如果真实头颅质量为8kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N.
(2)请解释:为什么低头角度越大,颈部肌肉的拉力会越大?答 .
(3)请你就预防和延缓颈椎损伤提出一个合理化的建议: .
试题篮
()