已知函数f(x)=x2+2x+alnx(a∈R).
(1)当时a=﹣4时,求f(x)的最小值;
(2)若函数f(x)在区间(0,1)上为单调函数,求实数a的取值范围.
(1)函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
(2)已知函数f(x)是定义在R上的偶函数,当x≤0时,f(x)=x(x+1),则f(x)的解析式为f(x)=x2﹣|x|;
(3)若loga >1,则a的取值范围是(
>1,则a的取值范围是( ,1);
,1);
(4)若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),则x+y<0.
其中所有正确命题的序号是 .
对于函数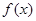 ,若在定义域内存在实数
,若在定义域内存在实数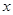 ,满足
,满足 ,则称为“局部奇函数”
,则称为“局部奇函数”
(1)已知二次函数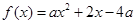 (
( 且
且 ),试判断
),试判断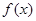 是否为“局部奇函数”,并说明理由;
是否为“局部奇函数”,并说明理由;
(2)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数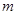 的取值范围;
的取值范围;
(3)若 为定义域为
为定义域为 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数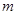 的取值范围;
的取值范围;
函数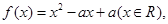 数列
数列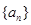 的前
的前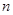 项和
项和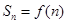 ,且
,且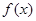 同时满足:①不等式
同时满足:①不等式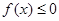 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在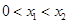 ,使得不等式
,使得不等式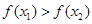 成立.
成立.
(1)求函数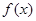 的表达式;
的表达式;
(2)求数列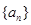 的通项公式.
的通项公式.
试题篮
()