初中数学一次函数的应用试题

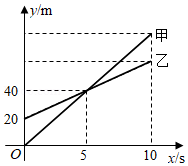
甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某公司生产的一种营养品信息如表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．

营养品信息表
营养成份	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
$A$ 包装	1千克	45元
$B$ 包装	0.25千克	12元

（1）问甲、乙两种食材每千克进价分别是多少元？

（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完．

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出．若 $A$ 的数量不低于 $B$ 的数量，则 $A$ 为多少包时，每日所获总利润最大？最大总利润为多少元？

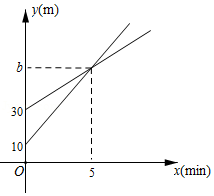
Ⅰ号无人机从海拔 $10m$ 处出发，以 $10m/\mathit{min}$ 的速度匀速上升，Ⅱ号无人机从海拔 $30m$ 处同时出发，以 $a(m/\mathit{min})$ 的速度匀速上升，经过 $5\mathit{min}$ 两架无人机位于同一海拔高度 $b\left(m\right)$ ．无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系如图．两架无人机都上升了 $15\mathit{min}$ ．

（1）求 $b$ 的值及Ⅱ号无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系式；

（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

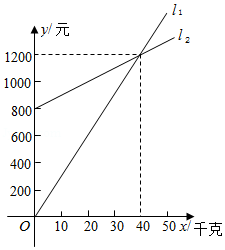
某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元     $)$	20	56	266
每月免费使用流量（兆     $)$	1024	$m$	无限
超出后每兆收费（元     $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程 $s$ （千米）与行驶时间 $t$ （小时）的关系如图所示（中途休息、加油的时间不计）．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升 $/$ 千米，请根据图象解答下列问题：

（1）写出工厂离目的地的路程；

（2）求 $s$ 关于 $t$ 的函数表达式；

（3）当货车显示加油提醒后，问行驶时间 $t$ 在怎样的范围内货车应进站加油？

某鲜花销售公司每月付给销售人员的工资有两种方案．

方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成．

如图中的射线 $l_1$ ，射线 $l_2$ 分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资 $y_1$ （单位：元）和 $y_2$ （单位：元）与其当月鲜花销售量 $x$ （单位：千克） $(x⩾0)$ 的函数关系．

（1）分别求 $y_1$ 、 $y_2$ 与 $x$ 的函数解析式（解析式也称表达式）；

（2）若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过2000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？

在"看图说故事"活动中，某学习小组结合图象设计了一个问题情境．已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $12\mathit{km}$ ，陈列馆离学校 $20\mathit{km}$ ．李华从学校出发，匀速骑行 $0.6h$ 到达书店；在书店停留 $0.4h$ 后，匀速骑行 $0.5h$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $0.5h$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $y\mathit{km}$ 与离开学校的时间 $xh$ 之间的对应关系．

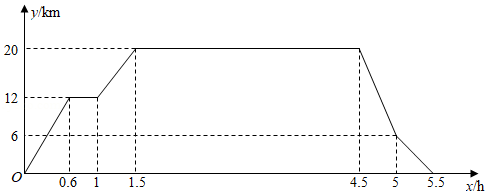
请根据相关信息，解答下列问题：

（Ⅰ）填表：

离开学校的时间     $/h$	0.1	0.5	0.8	1	3
离学校的距离     $/\mathit{km}$	2	10		12

（Ⅱ）填空：

①书店到陈列馆的距离为 　　 $\mathit{km}$ ；

②李华在陈列馆参观学习的时间为 　　 $h$ ；

③李华从陈列馆回学校途中，减速前的骑行速度为 　　 $\mathit{km}/h$ ；

④当李华离学校的距离为 $4\mathit{km}$ 时，他离开学校的时间为 　　 $h$ ．

（Ⅲ）当 $0⩽x⩽1.5$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

某品牌鞋子的长度 $\mathit{ycm}$ 与鞋子的"码"数 $x$ 之间满足一次函数关系．若22码鞋子的长度为 $16\mathit{cm}$ ，44码鞋子的长度为 $27\mathit{cm}$ ，则38码鞋子的长度为 $($ 　　 $)$

A．

$23\mathit{cm}$

B．

$24\mathit{cm}$

C．

$25\mathit{cm}$

D．

$26\mathit{cm}$

某药店选购了一批消毒液，进价为每瓶10元，在销售过程中发现，每天销售量 $y$（瓶 $)$与每瓶售价 $x$（元 $)$之间存在一次函数关系（其中 $10⩽x⩽21$，且 $x$为整数）．当每瓶消毒液售价为12元时，每天销售量为90瓶；当每瓶消毒液售价为15元时，每天销售量为75瓶．

（1）求 $y$与 $x$之间的函数关系式；

（2）设该药店销售该消毒液每天的销售利润为 $w$元，当每瓶消毒液售价为多少元时，药店销售该消毒液每天销售利润最大，最大利润是多少元？

超市购进某种苹果，如果进价增加2元 $/$千克要用300元；如果进价减少2元 $/$千克，同样数量的苹果只用200元．

（1）求苹果的进价；

（2）如果购进这种苹果不超过100千克，就按原价购进；如果购进苹果超过100千克，超过部分购进价格减少2元 $/$千克，写出购进苹果的支出 $y$（元 $)$与购进数量 $x$（千克）之间的函数关系式；

（3）超市一天购进苹果数量不超过300千克，且购进苹果当天全部销售完，据统计，销售单价 $z$（元 $/$千克）与一天销售数量 $x$（千克）的关系为 $z=-\frac{1}{100}x+12$．在（2）的条件下，要使超市销售苹果利润 $w$（元 $)$最大，求一天购进苹果数量．（利润 $=$销售收入 $-$购进支出）

国庆节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示．

	甲	乙
进价（元/千克）	x	x+4
售价（元/千克）	20	25

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同．

（1）求x的值；

（2）若超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，则超市应如何进货才能获得最大利润，最大利润是多少？

渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元 $/$千克，根据市场调查发现，批发价定为48元 $/$千克时，每天可销售500千克，为增大市场占有率，在保证盈利的情况下，工厂采取降价措施，批发价每千克降低1元，每天销量可增加50千克．

（1）写出工厂每天的利润 $W$元与降价 $x$元之间的函数关系．当降价2元时，工厂每天的利润为多少元？

（2）当降价多少元时，工厂每天的利润最大，最大为多少元？

（3）若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

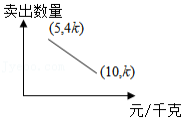
某人购进一批苹果到集贸市场零售，已知卖出的苹果数量与售价之间的关系如图所示，成本5元 $/$ 千克，现以8元卖出，挣得 　　元．

在一次机器"猫"抓机器"鼠"的展演测试中，"鼠"先从起点出发， $1\mathit{min}$ 后，"猫"从同一起点出发去追"鼠"，抓住"鼠"并稍作停留后，"猫"抓着"鼠"沿原路返回．"鼠"、"猫"距起点的距离 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 之间的关系如图所示．

（1）在"猫"追"鼠"的过程中，"猫"的平均速度与"鼠"的平均速度的差是 　　 $m/\mathit{min}$ ；

（2）求 $\mathit{AB}$ 的函数表达式；

（3）求"猫"从起点出发到返回至起点所用的时间．

公路上正在行驶的甲车，发现前方 $20m$ 处沿同一方向行驶的乙车后，开始减速，减速后甲车行驶的路程 $s$ （单位： $m)$ 、速度 $v$ （单位： $m/s)$ 与时间 $t$ （单位： $s)$ 的关系分别可以用二次函数和一次函数表示，其图象如图所示．

（1）当甲车减速至 $9m/s$ 时，它行驶的路程是多少？

（2）若乙车以 $10m/s$ 的速度匀速行驶，两车何时相距最近，最近距离是多少？