如图1，在Rt△AOB中，∠AOB=90°，AO=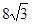，∠ABO=30°．动点P在线段AB上从点A向终点B以每秒个单位的速度运动，设运动时间为t秒．在直线OB 上取两点M、N作等边△PMN．
（1）求当等边△PMN的顶点M运动到与点O重合时t的值．
（2）求等边△PMN的边长（用t的代数式表示）；
（3）如果取OB的中点D，以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE，点C在线段AB上．设等边△PMN和矩形ODCE重叠部分的面积为S，请求出当0≤t≤2秒时S与t的函数关系式，并求出S的最大值．
（4）在（3）中，设PN与EC的交点为R，是否存在点R，使△ODR是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．