如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=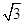 .
.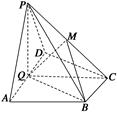
(1)若点M是棱PC的中点,求证:PA∥平面BMQ;
(2)若二面角M—BQ—C为30°,设PM=tMC,试确定t的值.
相关知识点
推荐试卷
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=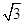 .
.
(1)若点M是棱PC的中点,求证:PA∥平面BMQ;
(2)若二面角M—BQ—C为30°,设PM=tMC,试确定t的值.
试题篮
()