函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f′(x)=0的两根为x1,x2,则|x1﹣x2|的取值范围是( )
A.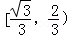 |
B.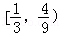 |
C.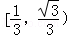 |
D.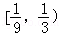 |
推荐试卷
函数f(x)=ax3+bx2+cx+d(a≠0),若a+b+c=0,导函数f′(x)满足f′(0)f′(1)>0,设f′(x)=0的两根为x1,x2,则|x1﹣x2|的取值范围是( )
A.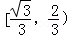 |
B.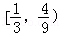 |
C.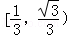 |
D.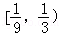 |
试题篮
()