在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是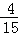 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
推荐试卷
在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是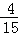 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
试题篮
()