(本小题满分13分).已知点A、B的坐标分别为( ,0)、(2,0),直线AT、BT交于点T,且它们的斜率之积为常数
,0)、(2,0),直线AT、BT交于点T,且它们的斜率之积为常数 ,点T的轨迹以及A、B两点构成曲线C.
,点T的轨迹以及A、B两点构成曲线C.
(Ⅰ)求曲线C的方程,并求其焦点坐标;
(Ⅱ)若 ,且曲线C上的点到其焦点的最小距离为1.设直线l:
,且曲线C上的点到其焦点的最小距离为1.设直线l: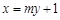 交曲线C于M、N,直线AM、BN交于点P.
交曲线C于M、N,直线AM、BN交于点P.
(ⅰ)当m = 0时,求点P的坐标;
(ⅱ)当m变化时,是否存在直线l1,使P总在直线l1上?若存在,求出l1的方程;若不存在,请说明理由.
推荐试卷
(本小题满分13分).已知点A、B的坐标分别为( ,0)、(2,0),直线AT、BT交于点T,且它们的斜率之积为常数
,0)、(2,0),直线AT、BT交于点T,且它们的斜率之积为常数 ,点T的轨迹以及A、B两点构成曲线C.
,点T的轨迹以及A、B两点构成曲线C.
(Ⅰ)求曲线C的方程,并求其焦点坐标;
(Ⅱ)若 ,且曲线C上的点到其焦点的最小距离为1.设直线l:
,且曲线C上的点到其焦点的最小距离为1.设直线l: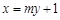 交曲线C于M、N,直线AM、BN交于点P.
交曲线C于M、N,直线AM、BN交于点P.
(ⅰ)当m = 0时,求点P的坐标;
(ⅱ)当m变化时,是否存在直线l1,使P总在直线l1上?若存在,求出l1的方程;若不存在,请说明理由.
试题篮
()