已知:如图,点B、F、E、C在同一条直线上,AB∥CD,且AB=CD,BF=CE.
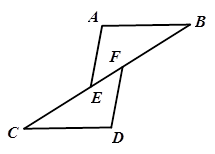
求证:∠AEB=∠DFC.
证明:∵AB∥CD(已知),
∴∠B=∠C( ).
∵BF=CE(已知),
∴BF+______=CE+______,即BE=CF.
在△ABE和△DCF中,
∵
∴△ABE≌△DCF( ).
∴∠AEB=∠DFC.
相关知识点
推荐试卷
已知:如图,点B、F、E、C在同一条直线上,AB∥CD,且AB=CD,BF=CE.

求证:∠AEB=∠DFC.
证明:∵AB∥CD(已知),
∴∠B=∠C( ).
∵BF=CE(已知),
∴BF+______=CE+______,即BE=CF.
在△ABE和△DCF中,
∵
∴△ABE≌△DCF( ).
∴∠AEB=∠DFC.
试题篮
()