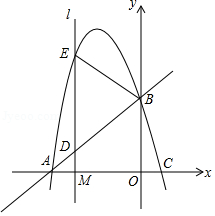
如图,抛物线 , 、 为常数)与 轴交于 、 两点,与 轴交于 点,直线 的函数关系式为 .
(1)求该抛物线的函数关系式与 点坐标;
(2)已知点 是线段 上的一个动点,过点 作 轴的垂线 分别与直线 和抛物线交于 、 两点,当 为何值时, 恰好是以 为底边的等腰三角形?
(3)在(2)问条件下,当 恰好是以 为底边的等腰三角形时,动点 相应位置记为点 ,将 绕原点 顺时针旋转得到 (旋转角在 到 之间);
.探究:线段 上是否存在定点 不与 、 重合),无论 如何旋转, 始终保持不变.若存在,试求出 点坐标;若不存在,请说明理由;
.试求出此旋转过程中, 的最小值.
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号