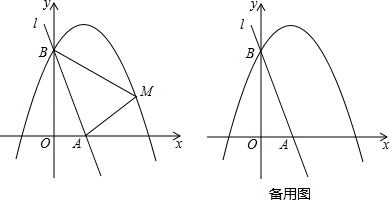
如图,直线 与 轴、 轴分别相交于 、 两点,抛物线 经过点 .
(1)求该抛物线的函数表达式;
(2)已知点 是抛物线上的一个动点,并且点 在第一象限内,连接 、 ,设点 的横坐标为 , 的面积为 ,求 与 的函数表达式,并求出 的最大值;
(3)在(2)的条件下,当 取得最大值时,动点 相应的位置记为点 .
①写出点 的坐标;
②将直线 绕点 按顺时针方向旋转得到直线 ,当直线 与直线 重合时停止旋转,在旋转过程中,直线 与线段 交于点 ,设点 、 到直线 的距离分别为 、 ,当 最大时,求直线 旋转的角度(即 的度数).
相关知识点
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号