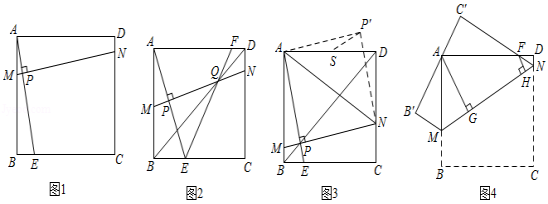
问题情境:如图1,在正方形 中, 为边 上一点(不与点 、 重合),垂直于 的一条直线 分别交 、 、 于点 、 、 .判断线段 、 、 之间的数量关系,并说明理由.
问题探究:在“问题情境”的基础上.
(1)如图2,若垂足 恰好为 的中点,连接 ,交 于点 ,连接 ,并延长交边 于点 .求 的度数;
(2)如图3,当垂足 在正方形 的对角线 上时,连接 ,将 沿着 翻折,点 落在点 处,若正方形 的边长为4, 的中点为 ,求 的最小值.
问题拓展:如图4,在边长为4的正方形 中,点 、 分别为边 、 上的点,将正方形 沿着 翻折,使得 的对应边 恰好经过点 , 交 于点 .分别过点 、 作 , ,垂足分别为 、 .若 ,请直接写出 的长.
推荐试卷








 粤公网安备 44130202000953号
粤公网安备 44130202000953号