（本小题满分12分）某校对参加高校自主招生测试的学生进行模拟训练，从中抽出N名学生，其数学成绩的频率分布直方图如图所示．已知成绩在区间[90，100]内的学生人数为2人。
（1）求N的值并估计这次测试数学成绩的平均分和众数；
（2）学校从成绩在[70，100]的三组学生中用分层抽样的方法抽取12名学生进行复试，若成绩在[80，90）这一小组中被抽中的学生实力相当，且能通过复试的概率均为
，设成绩在[80，90）这一小组中被抽中的学生中能通过复试的人数为
，求的分布列和数学期望．
（本小题满分13分）
某大学志愿者协会有10名同学，成员构成如下表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“数学专业”的概率为
．
| 专业 性别 |
中文 |
英语 |
数学 |
体育 |
| 男 |
 |
1 |
 |
1 |
| 女 |
1 |
1 |
1 |
1 |
现从这10名同学中随机选取3名同学参加社会公益活动（每位同学被选到的可能性相同）．
（Ⅰ）求
的值；
（Ⅱ）求选出的3名同学恰为专业互不相同的男生的概率；
（Ⅲ）设
为选出的3名同学中“女生或数学专业”的学生的人数，求随机变量的分布列及其数学期望
．
（本小题满分12分）退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势．某机构
为了解某城市市民的年龄构成，从该城市市民中随机抽取年龄段在20~80岁（含20岁和80岁）之间的600
人进行调查，并按年龄层次[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]绘制频率分布直方
图，如图所示．若规定年龄分布在[20，40）岁的人为“青年人”，[40，60）为“中年人”， [60，80]为“老年人”．
 |
（1）若每一组数据的平均值用该区间中点值来代替，试估算所调查的600人的平均年龄；
（2）将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率．从该城市20-80年龄段市民中
随机抽取3人，记抽到“老年人”的人数为
，求随机变量的分布列和数学期望．
(本题满分12分)
“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
 |
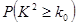0．10 |
0．05 |
0．010 |
0．005 |
 |
2．706 |
3．841 |
6．635 |
7．879 |
现计划在这次场外调查中按年龄段选取9名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
（参考公式：
其中
）
（本小题满分12分）
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取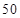
个作为样本,称出它们的重量（单位：克）,重量分组区间为
,
,
,
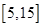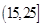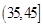,由此得到样本的重量频率分布直方图（如下图）,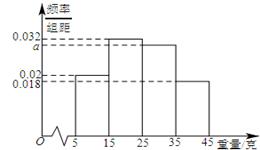
（1）求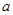
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值；
（2）从盒子中随机抽取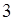
个小球,其中重量在
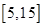内的小球个数为
,求的分布列和数学期望. (以直方图中的频率作为概率).
(本题满分10分)
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示，其中年龄分组区间是：
．
（1）求图中
的值并根据频率分布直方图估计这500名志愿者中年龄在
岁的人数；
（2）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人，记这3名志愿者中“年龄低于35岁”的人数为
，求的分布列及数学期望．
（本小题满分12分）
某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(Ⅰ)从统计数据看，甲乙两个班哪个班成绩更稳定（用数据说明）？
(Ⅱ) 若把上表数据作为学生投篮命中率，规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作
和
，试求和的分布列和数学期望.
甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；
（2）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；
（3）若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为
，求的分布列及数学期望
．
（本小题满分12分）甲、乙两名射击运动员参加射击选拔训练，在相同的条件下，两人5次训练的成绩如下表（单位：环）
| 次数 |
1 |
2 |
3 |
4 |
5 |
| 甲 |
6．5 |
10．2 |
10．5 |
8．6 |
6．8 |
| 乙 |
10．0 |
9．5 |
9．8 |
9．5 |
7．0 |
（1）请画出茎叶图，从稳定性考虑，选派谁更好呢？说明理由（不用计算）。若从甲、乙两人5次成绩中各随机抽取一次，求抽取的成绩至少有一个低于9．0环的概率；
（2）若从甲、乙两人5次成绩中各随机抽取二次，设抽到10．0环以上（包括10．0环）的次数为
，求随机变量的分布列和期望；
（本小题满分13分）在一次抽奖活动中，有甲、乙等7人获得抽奖的机会。抽奖规则如下：主办方先从7人中随机抽取两人均获奖1000元，再从余下的5人中随机抽取1人获奖600元，最后还从这5人中随机抽取1人获奖400元。
（Ⅰ）求甲和乙都不获奖的概率；
（Ⅱ）设X是甲获奖的金额，求X的分布列和均值
。
现有一大批种子，其中优良种占30℅，从中任取8粒，记X为8粒种子中的优质良种粒数，则X的期望是： ．
医生的专业能力参数
可有效衡量医生的综合能力，越大，综合能力越强，并规定: 能力参数不少于30称为合格，不少于50称为优秀．某市卫生管理部门随机抽取300名医生进行专业能力参数考核，得到如图所示的能力的频率分布直方图:
（Ⅰ）求出这个样本的合格率、优秀率；
（Ⅱ）现用分层抽样的方法从中抽出一个样本容量为20的样本，再从这20名医生中随机选出2名．
①求这2名医生的能力参数为同一组的概率；
②设这2名医生中能力参数为优秀的人数为
，求随机变量的分布列和期望．
（本小题满分12分）我国新修订的《环境空气质量标准》指出空气质量指数在
为优秀，各类人群可正常活动．市环保局对我市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为
，
，
，
，由此得到样本的空气质量指数频率分布直方图，如图．
（1）求
的值；
（2）根据样本数据，试估计这一年度的空气质量指数的平均值；
（3）如果空气质量指数不超过
，就认定空气质量为“特优等级”，则从这一年的监测数据中随机抽取
天的数值，其中达到“特优等级”的天数为
，求的分布列和数学期望．
为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》，某驾校将小型汽车驾照考试科目二的培训测试调整为：从10个备选测试项目中随机抽取4个，只有选中的4个项目均测试合格，科目二的培训才算通过．已知甲对10个测试项目测试合格的概率均为
；乙对其中8个测试项目完全有合格把握，而另2个测试项目却根本不会．
（Ⅰ）求甲恰有2个测试项目合格的概率；
（Ⅱ）记乙的测试项目合格数为
，求的分布列及数学期望
．
试题篮
()
粤公网安备 44130202000953号
