高中数学随机思想的发展试题

（本小题满分12分）甲、乙两人对弈棋局，甲胜、乙胜、和棋的概率都是，规定有一方累计2胜或者累计2和时，棋局结束。棋局结束时，若是累计两和的情形，则宣布甲乙都获得冠军；若一方累计2胜，则宣布该方获得冠军，另一方获得亚军。设结束时对弈的总局数为X．
（1）设事件A：“X=3且甲获得冠军”，求A的概率；
（2）求X的分布列和数学期望。

（本小题满分12分） 甲、乙两人轮流投篮,每人每次投一球,．约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束．设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响．
（Ⅰ） 求甲获胜的概率;
（Ⅱ） 求投篮结束时甲的投篮次数的分布列与期望

某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．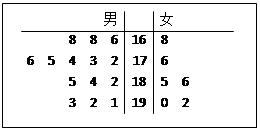

（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，再从这8人中选3人，那么至少有一人是甲部门人选的概率是多少？
（2）若从所有甲部门人选中随机选3人，用X表示所选人员中能担任助理工作的人数，写出X的分布列，并求出X的数学期望．

为了分流地铁高峰的压力，某市发改委通过听众会，决定实施低峰优惠票价制度.不超过公里的地铁票价如下表：

乘坐里程（单位：）
票价（单位：元）

现有甲、乙两位乘客，他们乘坐的里程都不超过公里.已知甲、乙乘车不超过公里的概率分别为，，甲、乙乘车超过公里且不超过公里的概率分别为， .
（Ⅰ）求甲、乙两人所付乘车费用不相同的概率；
（Ⅱ）设甲、乙两人所付乘车费用之和为随机变量，求的分布列与数学期望．

（本小题满分10分）袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为。现有甲、乙两人从袋中轮流、不放回地摸取1球，甲先取，乙后取，然后甲再取……直到袋中的球取完即终止。若摸出白球，则记2分，若摸出黑球，则记1分。每个球在每一次被取出的机会是等可能的。用x表示甲，乙最终得分差的绝对值．
(1)求袋中原有白球的个数；
(2)求随机变量x的概率分布列及期望Ex．

(本小题满分12分)
为了普及环保知识，增强环保意识，某校从理科甲班抽取60人，从文科乙班抽取50人参加环保知识测试.
（Ⅰ）根据题目条件完成下面2×2列联表，并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.

	优秀人数	非优秀人数	总计
甲班
乙班		30
总计	60

（Ⅱ）现已知三人获得优秀的概率分别为，设随机变量表示三人中获得优秀的人数，求的分布列及期望.附:， 

	0.100	0.050	0.025	0.010	0.005
	2.706	3.841	5.024	6.635	7.879

 

（本小题满分12分）国家AAAAA级八里河风景区五一期间举办“管仲杯”投掷飞镖比赛．每3人组成一队，每人投掷一次．假设飞镖每次都能投中靶面，且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”（靶面正方形如图所示,其中阴影区域的边界曲线近似为函数的图像）．每队有３人“成功” 获一等奖，２人“成功” 获二等奖，１人“成功” 获三等奖，其他情况为鼓励奖（即四等奖）（其中任何两位队员“成功”与否互不影响）．

（）求某队员投掷一次“成功”的概率；
（）设为某队获奖等次，求随机变量的分布列及其期望．

为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
（Ⅰ）设 $A$为事件"选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会"求事件 $A$发生的概率；
（Ⅱ）设 $X$为选出的4人中种子选手的人数，求随机变量 $X$的分布列和数学期望.

某市 $A,B$两所中学的学生组队参加辩论赛， $A$中学推荐3名男生，2名女生， $B$中学推荐了3名男生，4名女生，两校推荐的学生一起参加集训，由于集训后队员的水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队
（1）求 $A$中学至少有1名学生入选代表队的概率.
（2）某场比赛前，从代表队的6名队员中随机抽取4人参赛，设 $X$表示参赛的男生人数，求 $X$得分布列和数学期望.

赌博有陷阱．某种赌博每局的规则是：赌客先在标记有1,2,3,4,5的卡片中随机摸取一张，将卡片上的数字作为其赌金（单位：元）；随后放回该卡片，再随机摸取两张，将这两张卡片上数字之差的绝对值的1.4倍作为其奖金（单位：元）．若随机变量 ${\zeta }_1$和 ${\zeta }_2$分别表示赌客在一局赌博中的赌金和奖金，则 $E{\zeta }_1-E{\zeta }_2=$（元）．

若 $n$是一个三位正整数，且 $n$的个位数字大于十位数字，十位数字大于百位数字，则称 $n$为"三位递增数"（如137,359,567等）.在某次数学趣味活动中，每位参加者需从所有的"三位递增数"中随机抽取1个数，且只能抽取一次.得分规则如下：若抽取的"三位递增数"的三个数字之积不能被5整除，参加者得0分；若能被5整除，但不能被10整除，得-1分；若能被10整除，得1分.
（Ⅰ）写出所有个位数字是5的"三位递增数" ；
（Ⅱ）若甲参加活动，求甲得分 $X$的分布列和数学期望 $EX$.

某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球，在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖.
（1）求顾客抽奖1次能获奖的概率；
（2）若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为，求的分布列和数学期望.

某厂用鲜牛奶在某台设备上生产 $A,B$ 两种奶制品．生产1吨 $A$ 产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨 $B$ 产品需鲜牛奶1．5吨，使用设备1．5小时，获利1200元．要求每天 $B$ 产品的产量不超过 $A$ 产品产量的2倍，设备每天生产 $A,B$ 两种产品时间之和不超过12小时．假定每天可获取的鲜牛奶数量 $W$ （单位：吨）是一个随机变量，其分布列为

该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利 $Z$ （单位：元）是一个随机变量．

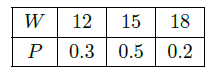
（Ⅰ）求 $Z$ 的分布列和均值；
（Ⅱ）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．

已知2件次品和3件正品放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测结束.
（Ⅰ）求第一次检测出的是次品且第二次检测出的是正品的概率；
（Ⅱ）已知每检测一件产品需要费用100元，设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用（单位：元），求的分布列和均值（数学期望）.

（本小题满分12 分）某理科考生参加自主招生面试，从7道题中（4道理科题3道文科题）不放回地依次任取3道作答．
（1）求该考生在第一次抽到理科题的条件下，第二次和第三次均抽到文科题的概率；
（2）规定理科考生需作答两道理科题和一道文科题，该考生答对理科题的概率均为，答对文科题的概率均为，若每题答对得10分，否则得零分．现该生已抽到三道题（两理一文），求其所得总分的分布列与数学期望．