下列有关命题的说法中错误的是( )
A.若 为假命题,则 为假命题,则 、 、 均为假命题. 均为假命题. |
B.“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
C.命题“若 则 则 ”的逆否命题为:“若 ”的逆否命题为:“若 则 则 ”. ”. |
D.对于命题 使得 使得 <0,则 <0,则 ,使 ,使 . . |
命题“存在 R,
R,
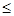 0”的否定是( ).
0”的否定是( ).
A.不存在 R, R,  >0 >0 |
B.存在 R, R,  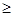 0 0 |
C.对任意的 R, R,  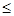 0 0 |
D.对任意的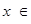 R, R,  >0 >0 |
某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<,那么它的假设应该是( ).
| A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥” |
| B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥” |
| C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥” |
| D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥” |
已知命题p:“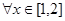 都有x2
都有x2 a”。命题q:“
a”。命题q:“ ,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )
,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )
A.a |
B.-2<a<1 | C.a≤-2或a=1 | D.a |
以下四个命题中,真命题的个数是( )
①命题“若 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
②若 为假命题,则
为假命题,则 、
、 均为假命题;
均为假命题;
③命题 :存在
:存在 ,使得
,使得 ,则
,则 :任意
:任意 ,都有
,都有 ;④在
;④在 中,
中, 是
是 的充分不必要条件.
的充分不必要条件.
| A.1 | B.2 | C.3 | D.4 |
试题篮
()