如图, 中, , , ,以点 为圆心, 为半径作 ,当 时, 与 的位置关系是
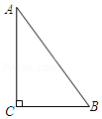
| A. |
相离 |
B. |
相切 |
C. |
相交 |
D. |
无法确定 |
如图,在平面直角坐标系中,与
轴的正半轴交于
、
两点,与
轴的正半轴相切于点
,连接
、
,已知
半径为2,
,双曲线
经过圆心
.
(1)求双曲线的解析式;
(2)求直线的解析式.

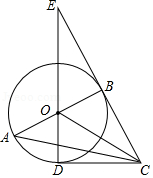
如图,在中,
,以
为直径作
,点
为
上一点,且
,连接
并延长交
的延长线于点
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,求圆的半径及
的长.
如图,已知 、 两点的坐标分别为 、 ,点 、 分别是直线 和 轴上的动点, ,点 是线段 的中点,连接 交 轴于点 ,当 面积取得最小值时, 的值是

| A. |
|
B. |
|
C. |
|
D. |
|
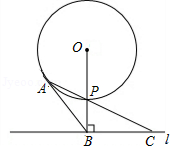
与
相切于点
,直线
与
相离,
于点
,且
,
与
交于点
,
的延长线交直线
于点
.
(1)求证:;
(2)若的半径为3,求线段
的长;
(3)若在上存在点
,使
是以
为底边的等腰三角形,求
的半径
的取值范围.
如图,直线与
相离,
于点
,与
相交于点
,
.
是直线
上一点,连结
并延长交
于另一点
,且
.
(1)求证:是
的切线;
(2)若的半径为3,求线段
的长.

如图,是
的外接圆,
的平分线交
于点
,交
于点
,过点
作直线
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,
,求
的长.

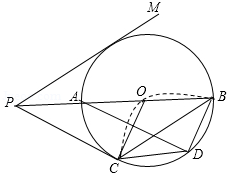
如图,为
的直径,点
为
上一点,将弧
沿直线
翻折,使弧
的中点
恰好与圆心
重合,连接
,
,
,过点
的切线与线段
的延长线交于点
,连接
,在
的另一侧作
.
(1)判断与
的位置关系,并说明理由;
(2)若,求四边形
的面积.
对于平面直角坐标系中的图形
,
,给出如下定义:
为图形
上任意一点,
为图形
上任意一点,如果
,
两点间的距离有最小值,那么称这个最小值为图形
,
间的“闭距离“,记作
.
已知点,
,
.
(1)求(点
,
;
(2)记函数的图象为图形
.若
,直接写出
的取值范围;
(3)的圆心为
,半径为1.若
,直接写出
的取值范围.
在平面直角坐标系中的点
和图形
,给出如下的定义:若在图形
上存在一点
,使得
、
两点间的距离小于或等于1,则称
为图形
的关联点.
(1)当的半径为2时,
①在点,
,
,
,
,
中,
的关联点是 .
②点在直线
上,若
为
的关联点,求点
的横坐标的取值范围.
(2)的圆心在
轴上,半径为2,直线
与
轴、
轴交于点
、
.若线段
上的所有点都是
的关联点,直接写出圆心
的横坐标的取值范围.
(年云南省曲靖市)如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,﹣2),A为OB的中点,以A为顶点的抛物线 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
(本小题5分)如图,在图中求作⊙P,使⊙P满足以线段MN为弦,且圆心P到∠AOB两边的距离相等(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)。
试题篮
()