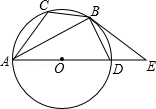
如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且 ,延长AD到E,且有 .
(1)求证:BE是⊙O的切线;
(2)若 , ,求圆的直径AD及切线BE的长.
如图,在△ ABC中, D、 E分别为 AB、 AC边上的点, , BE与 CD相交于点 F,则下列结论一定正确的是( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在△ ABC中,点 D是 AB边上的一点.
(1)请用尺规作图法,在△ ABC内,求作∠ ADE,使∠ ADE=∠ B, DE交 AC于 E;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若 =2,求 的值.

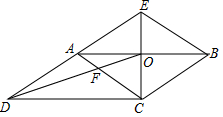
如图, CE是▱ ABCD的边 AB的垂直平分线,垂足为点 O, CE与 DA的延长线交于点 E.连接 AC, BE, DO, DO与 AC交于点 F,则下列结论:
①四边形 ACBE是菱形;
②∠ ACD=∠ BAE;
③ AF: BE=2:3;
④ S 四边形 AFOE: S △ COD=2:3.
其中正确的结论有 .(填写所有正确结论的序号)
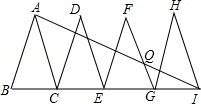
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .
如图, 已知正方形  ,点
,点 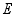 是
是 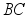 边的中点,
边的中点,  与
与 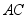 相交于点
相交于点 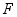 ,连接
,连接 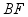 ,下列结论:①
,下列结论:① 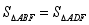 ;②
;②  ;③
;③ 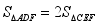 ;④
;④  ,其中正确的是
,其中正确的是 

| A. |
A .①③B .②③C .①④D .②④ |
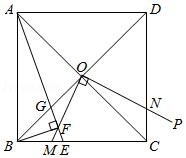
如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 于点 ,连接 并延长,交 于点 ,过点 作 交 于点 , ,现给出下列结论:① ;② ;③ ;④ ;其中正确的结论有
| A. |
①②③ |
B. |
②③④ |
C. |
①②④ |
D. |
①③④ |
如图,在 中, , , , 为 边上的动点(与 、 不重合), ,交 于点 ,连接 ,设 , 的面积为 .
(1)用含 的代数式表示 的长;
(2)求 与 的函数表达式,并求当 随 增大而减小时 的取值范围.

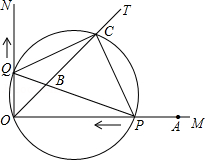
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
如图1,平面直角坐标系 中,等腰 的底边 在 轴上, ,顶点 在 的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点 从点 出发,以相同的速度沿 向左运动,到达点 停止.已知点 、 同时出发,以 为边作正方形 ,使正方形 和 在 的同侧,设运动的时间为 秒 .
(1)当点 落在 边上时,求 的值;
(2)设正方形 与 重叠面积为 ,请问是否存在 值,使得 ?若存在,求出 值;若不存在,请说明理由;
(3)如图2,取 的中点 ,连结 ,当点 、 开始运动时,点 从点 出发,以每秒 个单位的速度沿 运动,到达点 停止运动.请问在点 的整个运动过程中,点 可能在正方形 内(含边界)吗?如果可能,求出点 在正方形 内(含边界)的时长;若不可能,请说明理由.
试题篮
()