初中数学相似多边形的性质试题

已知两个相似三角形的周长比是1:3，它们的面积比是    

如图，等边△ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC上一点；若∠APD=60°，则CD长是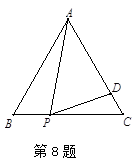

A．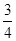

B．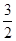

C．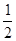

D．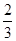

如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．已知，的顶点都在格点上，,,,若在边上以某个格点为端点画出长是的线段，使线段另一端点恰好落在边上，且线段与点C构成的三角形与相似，请你在图中画出线段（不必说明理由）

如图，平行四边形中，为的中点，的面积为2，则△  的面积为

A．2

B．4

C．6

D．8

如图①，△ABC中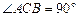，，∠ABC=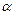，将△ABC绕点A顺时针旋转得到△AB ¢C ¢，设旋转的角度是．

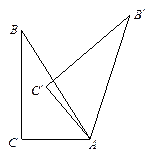
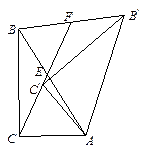
（1）如图②，当="      " °（用含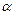的代数式表示）时，点B ¢恰好落在CA的延长线上；
（2）如图③，连结BB ¢、CC ¢， CC ¢的延长线交斜边AB于点E，交BB ¢于点F．请写出图中两对相似三角形                 ，               
（不含全等三角形），并选一对证明．

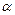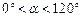含30°角的直角三角板ABC中，∠A=30°.将其绕直角顶点C顺时针旋转角（且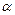≠ 90°），得到Rt△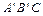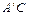，边与AB所在直线交于点D，过点 D作DE∥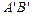交边于点E，连接BE.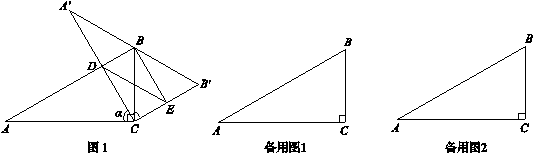

（1）如图1，当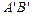边经过点B时，=      °；
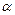（2）在三角板旋转的过程中，若∠CBD的度数是∠CBE度数的m倍，猜想m的值并证明你的结论；
（3） 设 BC=1，AD=x，△BDE的面积为S，以点E为圆心，EB为半径作⊙E，当S=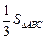
时，求AD的长，并判断此时直线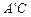与⊙E的位置关系.

已知：如图，在△ABC中，AB="AC=" 5，BC= 8，D，E分别为BC，AB边上一点，∠ADE=∠C．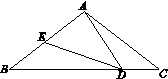

（1）求证：△BDE∽△CAD；
（2）若CD=2，求BE的长．

如图，在△ABC中，DE∥AB分别交AC，BC于点D，E，若AD=2，CD=3，则△CDE与△CAB的周长比为     

如图，将△ABC的三边分别扩大一倍得到△（顶点均在格点上），若它们是以P点为位似中心的位似图形，则P点的坐标是（    ）.

A．

B．

C．

D．

如图，在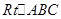中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为（   ）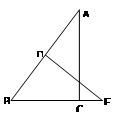

A．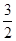

B．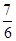

C．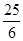

D．2

下列四个三角形，与左图中的三角形相似的是（   ）

在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′，则补充的这个条件是：（  ）

A．BC=B′C′

B．∠A=∠A′

C．AC=A′C′

D．∠C=∠C′

如下图，在△ABC中，∠ACB为直角，∠A=30°，CD⊥AB于D。若BD=1，则AB=_____

和是绕点旋转的两个相似三角形，其中与、与为对应角．

（1）如图1，若和分别是以与为顶角的等腰直角三角形，且两三角形旋转到使点、、在同一条直线上的位置时，请直接写出线段与线段的关系；
（2）若和为含有角的直角三角形，且两个三角形旋转到如图2的位置时，试确定线段与线段的关系，并说明理由；
（3）若和为如图3的两个三角形，且=，，在绕点旋转的过程中，直线与夹角的度数是否改变？若不改变，直接用含、的式子表示夹角的度数；若改变，请说明理由．

下图中的两个三角形是位似图形，它们的位似中心是   

A．点

B．点

C．点

D．点