为了考察两个变量 和
和 之间的线性相关性,甲、乙两同学各自独立地做
之间的线性相关性,甲、乙两同学各自独立地做 次和
次和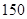 次试验,并且利用线性回归方法,求得回归直线分别为
次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两个人在试验中发现对变量
,已知两个人在试验中发现对变量 的观测值的平均值都是
的观测值的平均值都是 ,对变量
,对变量 的观测值的平均值都是
的观测值的平均值都是 ,那么下列说法正确的是()
,那么下列说法正确的是()
A. 和 和 有交点 有交点 |
B. 和 和 相交,但交点不是 相交,但交点不是 |
C. 和 和 必定重合 必定重合 |
D. 和 和 必定不重合 必定不重合 |
某商场的销售部经过市场调查发现,该商场的某种商品每日的销售量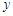 (单位:千克)与销售价格
(单位:千克)与销售价格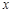 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
,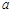 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(Ⅰ)求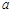 的值;
的值;
(Ⅱ)若该商品的成本为 元/千克,试确定销售价格
元/千克,试确定销售价格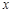 的值,使该商场每日销售该商品所获得的利润最大.
的值,使该商场每日销售该商品所获得的利润最大.
已知函数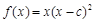 (
( )在
)在 处有极小值.
处有极小值.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在区间
在区间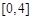 上的最大值和最小值.
上的最大值和最小值.
抛物线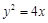 的焦点为
的焦点为 ,过点
,过点 的直线与该抛物线相交于
的直线与该抛物线相交于 两点,直线
两点,直线 分别交抛物线于点
分别交抛物线于点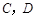 .若直线
.若直线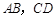 的斜率分别为
的斜率分别为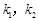 ,则
,则 _______.
_______.
曲线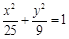 与曲线
与曲线 的( )
的( )
| A.长轴长相等 | B.短轴长相等 |
| C.焦距相等 | D.离心率相等 |
已知偶函数 (
(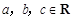 )在点
)在点 处的切线与直线
处的切线与直线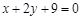 垂直,函数
垂直,函数 .
.
(Ⅰ)求函数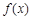 的解析式.
的解析式.
(Ⅱ)当 时,求函数
时,求函数 的单调区间和极值点;
的单调区间和极值点;
(Ⅲ)证明:对于任意实数x,不等式 恒成立.(其中e=2.71828…是自然对数的底数)
恒成立.(其中e=2.71828…是自然对数的底数)
如图所示, 和
和 两点分别在射线
两点分别在射线 (点
(点 ,
, 分别在第一,四象限)上移动,且
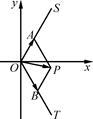
分别在第一,四象限)上移动,且 为坐标原点,动点
为坐标原点,动点 满足
满足 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求动点 的轨迹方程,并说明它表示什么曲线.
的轨迹方程,并说明它表示什么曲线.
某市有一个玉米种植基地.该基地的技术员通过种植实验发现,一种品质优良的玉米种子每粒发芽的概率都为0.95,现在该种植基地播种了10000粒这种玉米种子,对于没有发芽的种子,每粒需再播种1粒,补种的种子数记为 ,则
,则 的数学期望
的数学期望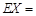 .
.
根据资阳市环保部门的空气质量监测资料表明,资阳市一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6.若资阳市某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
| A.0.45 | B.0.6 | C.0.75 | D.0.8 |
曲线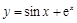 (其中e=2.71828…是自然对数的底数)在点
(其中e=2.71828…是自然对数的底数)在点 处的切线的斜率为( )
处的切线的斜率为( )
| A.2 | B.3 | C. |
D. |
(本小题满分12分)
已知向量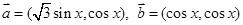 ,函数
,函数
(1)求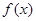 的单调递增区间;
的单调递增区间;
(2)当 时, 若
时, 若 求
求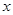 的值。
的值。
下面有五个命题:
①函数 的最小正周期是
的最小正周期是 ;
;
②终边在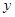 轴上的角的集合是
轴上的角的集合是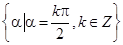 ;
;
③函数 ,在区间
,在区间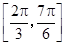 上是增函数;
上是增函数;
④若动直线 与函数
与函数 和
和 的图像分别交于
的图像分别交于 两点,则
两点,则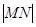 的最大值为1.
的最大值为1.
其中真命题的序号是 。
函数 的部分图象如图所示,则函数表达式为( )
的部分图象如图所示,则函数表达式为( )
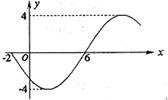
A. |
B.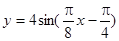 |
C. |
D. |
直线 与圆
与圆 相交于M,N两点,若
相交于M,N两点,若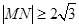 ,则
,则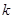 的取值范围是( )
的取值范围是( )
A. |
B. |
C.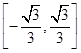 |
D. |
试题篮
()