如图,网格纸上绘制的是一个零件的三视图,网格小正方形的边长为
,则该零件的表面积为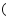

| A. |
|
B. |
|
C. |
|
D. |
|
已知抛物线方程 , 为焦点, 为抛物线准线上一点, 为线段 与抛物线的交点,定义: .
(1)当 时,求 ;
(2)证明:存在常数 ,使得 ;
(3) , , 为抛物线准线上三点,且 ,判断 与 的关系.
改革开放40年,我国卫生事业取得巨大成就,卫生总费用增长了数十倍.卫生总费用包括个人现在支出、社会支出、政府支出,如表为2012年 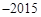 年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.
年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.
| 年份 |
卫生总费用(亿元) |
个人现金卫生支出 |
社会卫生支出 |
政府卫生支出 |
|||
| 绝对数(亿元) |
占卫生总费用比重 |
绝对数(亿元) |
占卫生总费用比重 |
绝对数(亿元) |
占卫生总费用比重 |
||
| 2012 |
28119.00 |
9656.32 |
34.34 |
10030.70 |
35.67 |
8431.98 |
29.99 |
| 2013 |
31668.95 |
10729.34 |
33.88 |
11393.79 |
35.98 |
9545.81 |
30.14 |
| 2014 |
35312.40 |
11295.41 |
31.99 |
13437.75 |
38.05 |
10579.23 |
29.96 |
| 2015 |
40974.64 |
11992.65 |
29.27 |
16506.71 |
40.29 |
12475.28 |
30.45 |
(数据来源于国家统计年鉴)
(1)指出2012年到2015年之间我国卫生总费用中个人现金支出占比和社会支出占比的变化趋势:
(2)设 表示1978年,第 年卫生总费用与年份 之间拟合函数 研究函数 的单调性,并预测我国卫生总费用首次超过12万亿的年份.
已知数列 , ,前 项和为 .
(1)若 为等差数列,且 ,求 ;
(2)若 为等比数列,且 ,求公比 的取值范围.
如图,在正三棱锥 中, , .
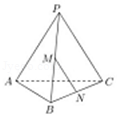
(1)若 的中点为 , 的中点为 ,求 与 的夹角;
(2)求 的体积.
以
,
为圆心的两圆均过
,与 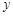 轴正半轴分别交于
,
,且满足
,则点
的轨迹是( )
轴正半轴分别交于
,
,且满足
,则点
的轨迹是( )
| A. |
直线 |
B. |
圆 |
C. |
椭圆 |
D. |
双曲线 |
已知平面 、 、 两两垂直,直线 、 、 满足: , , ,则直线 、 、 不可能满足以下哪种关系( )
| A. |
两两垂直 |
B. |
两两平行 |
C. |
两两相交 |
D. |
两两异面 |
已知 、 ,则" "是" "的( )
| A. |
充分非必要条件 |
B. |
必要非充分条件 |
C. |
充要条件 |
D. |
既非充分又非必要条件 |
试题篮
()