已知 , 函数 .
(1) 求曲线 在点 处的切线方程.
(2) 证明: 存在唯一的极值点.
(3) 若存在 , 使得 对任意 成立, 求实数 的取值范围.
若无穷数列 满足:只要 ,必有 ,则称 具有性质 .
(1)若 具有性质 ,且 , , , , ,求 ;
(2)若无穷数列 是等差数列,无穷数列 是公比为正数的等比数列, ; , ,判断 是否具有性质 ,并说明理由;
(3)设 是无穷数列,已知 ,求证:“对任意 , 都具有性质 ”的充要条件为“ 是常数列”.
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn=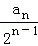 ,证明:数列{bn}是等差数列;
,证明:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn,
(3)设cn= ,求数列{cn}的最大项.
,求数列{cn}的最大项.
命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.
已知等差数列{an}的前n项和为Sn,且满足a2=4,a3+a4=17.
(1)求{an}的通项公式;
(2)设bn=2an+2,证明数列{bn}是等比数列并求其前n项和Tn.
试题篮
()