椭圆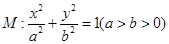 的离心率为
的离心率为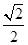 ,且过点
,且过点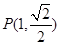 直线
直线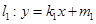 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线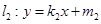 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形
(1)求椭圆M的方程;
(2)求证:平行四边形ABCD的对角线AC和BD相交于原点O;
(3)若平行四边形ABCD为菱形,求菱形ABCD的面积的最小值
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA 底面ABCD,且SA=2,AD=DC=1
底面ABCD,且SA=2,AD=DC=1
(1)若点E在SD上,且 证明:
证明: 平面
平面 ;
;
(2)若三棱锥S-ABC的体积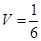 ,求面SAD与面SBC所成二面角的正弦值的大小
,求面SAD与面SBC所成二面角的正弦值的大小
过双曲线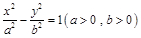 的一个焦点作实轴的垂线,交双曲线于
的一个焦点作实轴的垂线,交双曲线于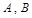 两点,若线段
两点,若线段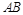 的长度恰等于焦距,则双曲线的离心率为( )
的长度恰等于焦距,则双曲线的离心率为( )
A.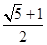 |
B.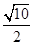 |
C.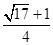 |
D.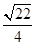 |
已知椭圆E: =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x= 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ⊥
⊥ ,求出该圆的方程.
,求出该圆的方程.
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按 米处理).
米处理).
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.
抛物线 的方程为
的方程为 ,过抛物线
,过抛物线 上一点
上一点 (
( )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线 于
于 两点(
两点( 三点互不相同),且满足
三点互不相同),且满足 (
( 且
且 ).
).
(1)求抛物线 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)设直线 上一点
上一点 ,满足
,满足 ,证明线段
,证明线段 的中点在
的中点在 轴上;
轴上;
(3)当 =1时,若点
=1时,若点 的坐标为
的坐标为 ,求
,求 为钝角时点
为钝角时点 的纵坐标
的纵坐标 的取值范围.
的取值范围.
已知 是等差数列,首项
是等差数列,首项 ,前
,前 项和为
项和为 .令
.令 ,
, 的前
的前 项和
项和 .数列
.数列 是公比为
是公比为 的等比数列,前
的等比数列,前 项和为
项和为 ,且
,且 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)证明: .
.
过椭圆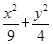 =1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
=1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
A.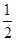 |
B.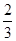 |
C.1 | D.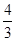 |
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: 、
、 、
、 、
、 .
.
(1)经判断点 ,
, 在抛物线
在抛物线 上,试求出
上,试求出 的标准方程;
的标准方程;
(2)求抛物线 的焦点
的焦点 的坐标并求出椭圆
的坐标并求出椭圆 的离心率;
的离心率;
(3)过 的焦点
的焦点 直线与椭圆
直线与椭圆 交不同两点
交不同两点 且满足
且满足 ,试求出直线的方程.
,试求出直线的方程.
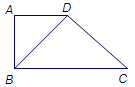
在直角梯形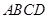 中,
中, ,
,
 ,
, ,如图,把
,如图,把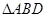 沿
沿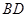 翻折,使得平面
翻折,使得平面 平面
平面 .
.


(1)求证: ;
;
(2)若点 为线段
为线段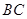 中点,求点
中点,求点 到平面
到平面 的距离;
的距离;
(3)在线段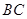 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面 所成角为
所成角为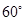 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知 .
.
(1)若 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;
(2)若 ,求证:当
,求证:当 时,
时, 恒成立;
恒成立;
(3)设 ,证明:
,证明: .
.
设函数f(x)=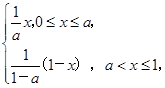 a为常数且a∈(0,1).
a为常数且a∈(0,1).
(1)当a=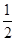 时,求f
时,求f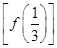 ;
;
(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[ ,
,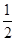 ]上的最大值和最小值.
]上的最大值和最小值.
试题篮
()