高中数学变量间的相关关系试题

下面是2×2列联表:

	y1	y2	总计
x1	a	21	73
x2	22	25	47
总计	b	46	120

则表中a,b的值分别为(　　)
(A)94,72        (B)52,50
(C)52,74        (D)74,52

在研究硝酸钠的可溶性程度时,在不同的温度下观测它在水中的溶解度,得观测结果如下:

温度(x)	0	10	20	50	70
溶解度(y)	66.7	76.0	85.0	112.3	128.0

则由此得到的回归直线的斜率是　　　　　　.

对一些城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查后知,y与x具有相关关系,满足回归方程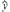=0.66x+1.562.若某被调查城市的居民人均消费水平为7.675(千元),则可以估计该城市人均消费额占人均工资收入的百分比约为　　　　%(结果保留两个有效数字).

对有线性相关关系的两个变量建立的回归直线方程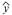=+x中,回归系数(　　)

A．不能小于0	B．不能大于0
C．不能等于0	D．只能小于0

对于给定的两个变量的统计数据,下列说法正确的是(　　)

A．都可以分析出两个变量的关系

B．都可以用一条直线近似地表示两者的关系

C．都可以作出散点图

D．都可以用确定的表达式表示两者的关系

下面两个变量间的关系不是函数关系的是(　　)

A．正方体的棱长与体积

B．角的度数与它的正弦值

C．单位产量为常数时,土地面积与粮食总产量

D．日照时间与水稻亩产量

某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是(    )

A．＝－10x＋200	B．＝10x＋200
C．＝－10x－200	D．＝10x－200

某农场给某种农作物施肥量x(单位：吨)与其产量y(单位：吨)的统计数据如下表：

施肥量x	2	3	4	5
产量y	26	39	49	54

根据上表，得到回归直线方程＝9.4x＋，当施肥量x＝6时，该农作物的预报产量是________．

某产品的广告费用与销售额的统计数据如下表：

广告费用x(万元)	4	2	3	5
销售额y(万元)	49	26	39	54

根据上表可得回归方程y=bx+a中的b为9.4，据此模型预报广告费用为6万元时销售额为（  ）
A．63.6万元    B．65.5万元   C． 67.7万元   D．72.0万元

某产品的广告费用x与销售额y的统计数据如下表：

广告费用x(万元)	3	4	5	6
销售额y(万元)	25	30	40	45

根据上表可得回归方程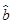＝x＋中的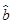为7.根据此模型，当预报广告费用为10万元时，销售额为________万元．

根据一组样本数据(x₁，y₁)，(x₂，y₂)，…，(x_n，y_n)的散点图分析存在线性相关关系，求得其回归方程＝0.85x－85.7，则在样本点(165，57)处的残差为(　　)

A．54.55

B．2.45

C．3.45

D．111.55

已知回归直线斜率的估计值为1.23，样本点的中心为点(4，5)，则回归直线的方程为(　　)

A．＝1.23x＋4	B．＝1.23x＋5
C．＝1.23x＋0.08	D．＝0.08x＋1.23

四名同学根据各自的样本数据研究变量之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
①与负相关且；  ②与负相关且；
③与正相关且；  ④与正相关且.
其中一定不正确的结论的序号是（   ）

A．①②

B．②③

C．③④

D．①④

为了判断高中三年级学生是否选修文科与性别的关系，现随机抽取50名学生，得到如下2×2列联表：

	理科	文科
男	13	10
女	7	20

已知P(K²≥3.841)≈0.05，P(K²≥5.024)≈0.025.
根据表中数据，得到k＝≈4.844.
则认为选修文科与性别有关系出错的可能性为________．

已知x与y之间的一组数据(如表所示)：则关于y与x的线性回归方程y＝bx＋a必过定点(　　)

A．(2,2)

B．(1.5,0)

C．(1,2)

D．(1.5,4)