某车间加工零件的数量 与加工时间
与加工时间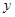 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间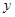 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
假设关于某设备的使用年限 和所支出的维修费
和所支出的维修费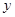 (万元)有如下的统计资料:
(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
由资料可知y和x呈线性相关关系,由表中数据算出线性回归方程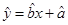 中的
中的 据此估计,使用年限为10年时的维修费用是 万元.
据此估计,使用年限为10年时的维修费用是 万元.
某商品的销售量 (件)与销售价格
(件)与销售价格 (元/件)存在线性相关关系,根据一组样本数据
(元/件)存在线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为 则下列结论正确的是( )
则下列结论正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.若 表示变量 表示变量 与 与 之间的线性相关系数,则 之间的线性相关系数,则 |
| C.当销售价格为10元时,销售量为100件 |
| D.当销售价格为10元时,销售量为100件左右 |
下列四个命题中,正确的是( )
A.已知 服从正态分布 服从正态分布 ,且 ,且 ,则 ,则 |
B.已知命题 ;命题 ;命题 .则命题“ .则命题“ ”是假命题 ”是假命题 |
C.设回归直线方程为 ,当变量 ,当变量 增加一个单位时, 增加一个单位时, 平均增加2个单位 平均增加2个单位 |
D.已知直线 , , ,则 ,则 的充要条件是 的充要条件是 =-3 =-3 |
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
根据以上数据建立一个2×2的列联表;
能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据: ,其中
,其中 .
.
| K2≥k0 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示
| |
积极参加班级工作 |
不太主动参加班级工作 |
| 学习积极性高 |
18 |
7 |
| 学习积极性一般 |
6 |
19 |
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由
附:
P( ≥k) ≥k) |
0.050 |
0.010 |
0.001 |
 = =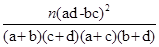 |
| k |
3.841 |
6.635 |
10.828 |
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积(m2) |
115 |
110 |
80 |
135 |
105 |
| 销售价格(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.
某车间为了规定工时定额, 需要确定加工零件所花费的时间, 为此进行了5次试验, 收集数
据如下:
| 加工零件数x(个) |
10 |
20 |
30 |
40 |
50 |
| 加工时间y(分钟) |
64 |
69 |
75 |
82 |
90 |
经检验, 这组样本数据具有线性相关关系, 那么对于加工零件的个数x与加工时间y这两个
变量, 下列判断正确的是( )
A.成正相关, 其回归直线经过点(30, 76)
B.成正相关, 其回归直线经过点(30, 75)
C.成负正相关, 其回归直线经过点(30, 76)
D.成负相关, 其回归直线经过点(30, 75)
下表是降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对应数据,根据表中提供的数据,可求出
(吨标准煤)的几组对应数据,根据表中提供的数据,可求出 关于
关于 的线性回归方程
的线性回归方程
 ,则表中
,则表中 的值为
的值为
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A. B.
B. C.
C. D.
D.
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x |
15 |
20 |
25 |
30 |
| 水稻产量y |
330 |
345 |
365 |
405 |
(1)试求出回归直线方程;
(2)请估计当施化肥量为10时,水稻产量为多少?
(已知:7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125)
某服装商场为了了解毛衣的月销售量 (件)与月平均气温
(件)与月平均气温 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 |
17 |
13 |
8 |
2 |
月销售量 (件) (件) |
24 |
33 |
40 |
55 |
(1)做出散点图;
(2) 求线性回归方程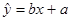 ;
;
(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(  ,
, )
)
某车间加工零件的数量 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
试题篮
()