已知回归直线的斜率的估计值为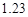 ,样本点的中心为
,样本点的中心为 ,则回归直线方程为
,则回归直线方程为
A.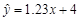 |
B.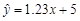 |
C.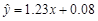 |
D. |
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
A.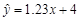 |
B.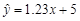 |
C. |
D. |
某车间加工零件的数量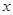 与加工时间
与加工时间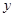 的统计数据如下表:
的统计数据如下表:
现已求得上表数据的回归方程 中的
中的 的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
| A.93分钟 | B.94分钟 | C.95分钟 | D.96分钟 |
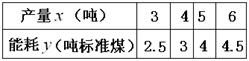
小明同学根据右表记录的产量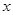 (吨)与能耗
(吨)与能耗 (吨标准煤)对应的四组数据,用最小二乘法求出了
(吨标准煤)对应的四组数据,用最小二乘法求出了 关于
关于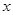 的线性回归方程
的线性回归方程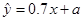 ,据此模型预报产量为7万吨时能耗为( )
,据此模型预报产量为7万吨时能耗为( )
A. |
B.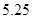 |
C. |
D.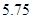 |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%,生铁成本平均每吨增加2元 |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为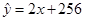 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%, 生铁成本平均每吨增加2元 |
某车间加工零件的数量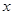 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数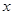 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程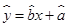 中的
中的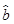 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
由一组数据(x1,y1)、(x2、y2)、 、(xn,yn)得到的线性回归方程为y=a+bx,则下列说法正确的是( )
A.直线y=a+bx必过点( , , ) ) |
| B.直线y=a+bx至少经过点(x1,y1)、(x2,y2)、 、(xn,yn)中的一点 |
| C.直线y=a+bx是由(x1,y1)、(x2、y2)、 、(xn,yn)中的两点确定的 |
| D.(x1,y1)、(x2,y2)、 、(xn、yn)这n个点到直线y=a+bx的距离之和最小 |
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是 :,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( )
:,且x1+x2+x3+…+x8=2(y1+y2+y3+…+y8)=6,则实数a的值是( )
A. |
B.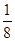 |
C. |
D. |
对变量x, y 有观测数据(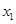 ,
,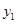 )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
一名小学生的年龄和身高(单位:cm)的数据如下:
| 年龄X |
6 |
7 |
8 |
9 |
| 身高Y |
118 |
126 |
136 |
144 |
由散点图可知,身高y与年龄x之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A. 154 B. 153 C. 152 D. 151
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大;
(2)若r<0,则x增大时,y也相应增大;
(3)若r=1或r=-1,则x与y的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上,其中正确的有 ( )
| A.①② | B.②③ | C.①③ | D.①②③ |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
| A.y=-10x+200 | B.y=10x+200 |
| C.y=-10x-200 | D.y=10x-200 |
已知一个线性回归方程为 =2x+45,其中x的取值依次为1, 7, 5, 13, 19,
=2x+45,其中x的取值依次为1, 7, 5, 13, 19,
则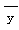 = ( )
= ( )
| A.58.5 | B.46.5 | C.63 | D.75 |
试题篮
()