随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图. 则甲班样本数据的众数和乙班样本数据的中位数分别是
| A.170,170 | B.171,171 | C.171,170 | D.170,172 |

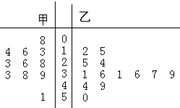
甲、已乙两名篮球运动员每场比赛的得分情况用茎叶图表示如下:则下列说法中正确的个数为
⑴甲得分的中位数为26,乙得分的中位数为36;
⑵甲、乙比较,甲的稳定性更好;
⑶乙有 的叶集中在茎3上
的叶集中在茎3上
⑷甲有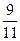 的叶集中在茎1、2、3上。
的叶集中在茎1、2、3上。
| A.1 | B.2 | C.3 | D.4 |
以下结论不正确的是 ( )
| A.根据2×2列联表中的数据计算得出K2≥6.635, 而P(K2≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系 |
| B.在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r| 越小,相关程度越小 |
| C.在回归分析中,相关指数R2越大,说明残差平方和越小,回归效果越好 |
D.在回归直线 中,变量x=200时,变量y的值一定是15 中,变量x=200时,变量y的值一定是15 |
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
甲乙丙丁四位同学各自对 两变量的线性相关性进行分析,并用回归分析方法得到相关系数
两变量的线性相关性进行分析,并用回归分析方法得到相关系数 与残差平方和
与残差平方和 ,如右表则哪位同学的试验结果体现
,如右表则哪位同学的试验结果体现 两变量更强的线性相关性( )
两变量更强的线性相关性( )
| |
甲 |
乙 |
丙 |
丁 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A 甲 B 乙 C 丙 D 丁
如图是2010年我校主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为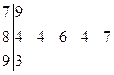
A. ,84 ,84 |
B. ,86 ,86 |
C.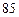 ,84 ,84 |
D.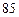 ,86 ,86 |
在相关分析中,对相关系数 ,下列说法正确的是
,下列说法正确的是
A. 越大,线性相关程度越强 越大,线性相关程度越强 |
B. 越小,线性相关程度越强 越小,线性相关程度越强 |
C. 越大,线性相关程度越弱, 越大,线性相关程度越弱, 越小,线性相关程度越强 越小,线性相关程度越强 |
D. 且 且 越接近 越接近 ,线性相关程度越强, ,线性相关程度越强, 越接近 越接近 ,线性相关程度越弱 ,线性相关程度越弱 |
废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
试题篮
()