某服装商场为了了解毛衣的月销售量 (件)与月平均气温
(件)与月平均气温 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 |
17 |
13 |
8 |
2 |
月销售量 (件) (件) |
24 |
33 |
40 |
55 |
(1)做出散点图;
(2) 求线性回归方程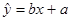 ;
;
(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(  ,
, )
)
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55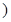 |
[55,65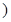 |
[65,75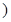 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| |
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
| 赞成 |
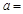 3 3 |
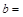 |
|
| 不赞成 |
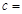 |
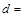 11 11 |
|
| 合计 |
|
|
50 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人赞成“楼市限购政策”的概率.
(参考公式: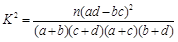 ,其中
,其中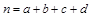 .)
.)
参考值表:
P(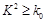 ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
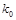 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本题满分14分) 假设关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用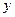 (万元)有如下的统计数据,由资料显示
(万元)有如下的统计数据,由资料显示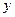 对
对 呈线性相关关系.
呈线性相关关系.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程。
(2)试根据(1)求出的线性回归方程,预测使用年限为10年时,维修费用是多少?
某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量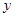 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线,
(单位:小时)之间近似满足如图所示的曲线,
(1)写出第一次服药后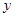 与
与 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到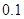 ,参考数据:
,参考数据: )
)
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
甲乙两个学校高三年级分别有1100人和1000人,为了了解这两个学校全体高三年级学生在该地区二模考试中的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统汁表,规定考试成绩在[120,150]内为优秀.
(I)试求x,y的值;
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。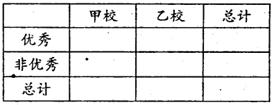
(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附:
(满分12分)甲、乙两名同学在高一学年中(相同条件下)都参加数学考试十次,每次考试成绩如下表:
 次 次 数 数同学 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
| 甲 |
90 |
50 |
70 |
80 |
70 |
60 |
80 |
60 |
70 |
70 |
| 乙 |
20 |
40 |
60 |
80 |
70 |
70 |
80 |
90 |
90 |
100 |
请在坐标系中画出甲、乙两同学的成绩折线 图,并
图,并 从以下不同角度对这次测试结果进行分析。
从以下不同角度对这次测试结果进行分析。
(1)从平均数和方差相结合看,分析谁的成绩更稳定些;
(2)从平均数和中位数相结合看,分析谁的成绩好些;
(3)从平均数和成绩为90分以上的次数相结合看,分析谁的成绩好些 ;
(4)从折线图上两人成绩分数的走势看,分析谁更有潜力。
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
(本题可以参考两个分类变量x和y有关系的可信度表:)
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
经过长期的观测得到:在交通繁忙的时段内,蚌埠市解放路某路段汽车的车流量 (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度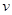 (
(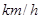 )之间的函数关系为
)之间的函数关系为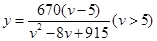 。
。
(1)在该时段内,当汽车的平均速度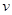 为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
(2)若要求在该时段内车流量超过10千辆/h,则汽车的平均速度应在什么范围内?
从某学校的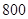 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于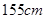 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组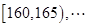 ,第八组
,第八组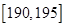 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人。
人。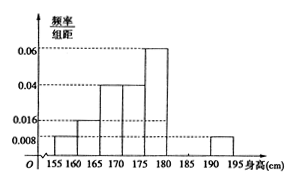
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的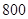 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在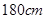 以上(含
以上(含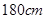 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件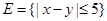 ,事件
,事件 ,求
,求
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x |
15 |
20 |
25 |
30 |
| 水稻产量y |
330 |
345 |
365 |
405 |
(1)试求出回归直线方程;
(2)请估计当施化肥量为10时,水稻产量为多少?
(已知:7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125)
试题篮
()