某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额x(千万元) |
3 |
5 |
6 |
7 |
9 9 |
| 利润额y(千万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性。
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
(本小题满分12分)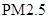 是指空气中直径小于或等于
是指空气中直径小于或等于 微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
微米的颗粒物(也称可入肺颗粒物).为了探究车流量与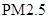 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与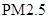 的数据如下表:
的数据如下表:
| 时间 |
周一 |
周二 |
周三 |
周四 |
周五 |
车流量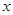 (万辆) (万辆) |
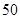 |
 |
 |
 |
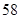 |
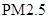 的浓度 的浓度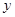 (微克/立方米) (微克/立方米) |
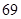 |
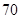 |
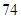 |
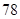 |
 |
(1)根据上表数据,请在下列坐标系中画出散点图;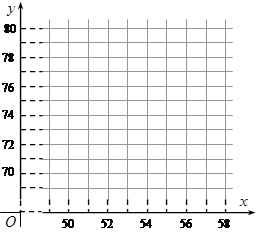
(2)根据上表数据,用最小二乘法求出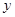 关于
关于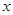 的线性回归方程
的线性回归方程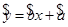 ;
;
(3)若周六同一时间段车流量是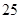 万辆,试根据(2)求出的线性回归方程预测,此时
万辆,试根据(2)求出的线性回归方程预测,此时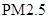 的浓度为多少(保留整数)?
的浓度为多少(保留整数)?
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出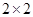 列联表,并判断是否有
列联表,并判断是否有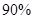 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
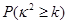 |
0.100 |
0.050 |
0.010 |
0.001 |
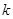 |
2.706 |
3.841 |
6.635 |
10.828 |
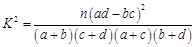 .
.
(本小题满分10分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出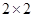 列联表,并判断是否有
列联表,并判断是否有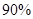 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
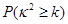 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
 .
.
在一次考试中,5名同学数学、物理成绩如下表所示:
| 学生 |
A |
B |
C |
D |
E |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)根据表中数据,求物理分 对数学分
对数学分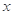 的回归方程:
的回归方程:
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以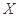 表示选中的同学中物理成绩高于90分的人数,求随机变量
表示选中的同学中物理成绩高于90分的人数,求随机变量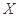 的分布列及数学期望
的分布列及数学期望 .(附:回归方程
.(附:回归方程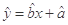 中,
中,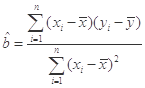 ,
, )
)
(本小题满分12分)某校为了提高学生身体素质,决定组建学校足球队,学校为了解报名学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为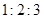 ,其中第2小组的频数为
,其中第2小组的频数为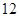 .
.
(Ⅰ)求该校报名学生的总人数;
(Ⅱ)若从报名的学生中任选3人,设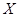 表示体重超过60kg的学生人数,求
表示体重超过60kg的学生人数,求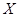 的数学期望与方差.
的数学期望与方差.
从某学校的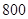 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于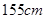 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组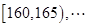 ,第八组
,第八组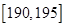 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人。
人。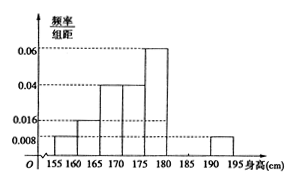
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的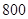 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在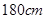 以上(含
以上(含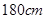 )的人数;
)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件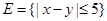 ,事件
,事件 ,求
,求
某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量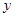 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线,
(单位:小时)之间近似满足如图所示的曲线,
(1)写出第一次服药后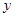 与
与 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到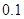 ,参考数据:
,参考数据: )
)
(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
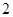 |
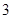 |
 |
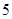 |
加工的时间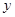 (小时) (小时) |
 |
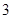 |
 |
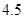 |
(1)在给定的坐标系中画出表中数据的散点图;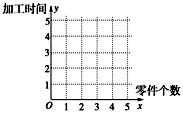
(2)求出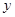 关于
关于 的线性回归方程
的线性回归方程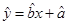 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工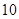 个零件需要多少时间?
个零件需要多少时间?
衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、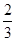 、
、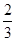 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量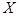 ,求随机变量
,求随机变量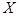 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
| 时间x |
1 |
2 |
3 |
4 |
5 |
| 命中率y |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
(本小题满分12分)某地区2007年至2013年农村居民家庭纯收入 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号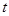 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求 关于
关于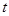 的线性回归方程;(已知b=0.5)
的线性回归方程;(已知b=0.5)
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
试题篮
()