调查了某地若干户家庭的年收x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,井由调查数据得到y对x的回归直线方程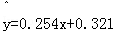 .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加 万元.
.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加 万元.
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
 =-0.7x+
=-0.7x+ ,则
,则 = .
= .
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如下的数据资料:
| 使用年限 |
x |
2 |
3 |
4 |
5 |
6 |
| 总费用 |
y |
2.3 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料,知y对x呈线性相关关系.试求:线性回归方程 =
=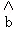 x+
x+ 的回归直线.
的回归直线. =
=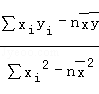 ,
, =
=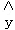 ﹣
﹣
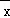 .
.
某池塘中野生水葫芦的面积与时间的函数关系的图象,如图所示.假设其关系为指数函数,并给出下列说法:

①此指数函数的底数为 ;
;
②在第 个月时,野生水葫芦的面积就会超过
个月时,野生水葫芦的面积就会超过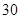
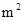 ;
;
③野生水葫芦从
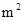 蔓延到
蔓延到
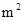 只需
只需 个月;
个月;
④设野生水葫芦蔓延到
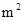 ,
,
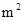 ,
,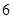
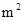 所需的时间分别为
所需的时间分别为 ,
, ,
,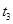 ,则有
,则有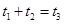 ;
;
⑤野生水葫芦在第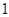 到第
到第 个月之间蔓延的平均速度等于在第
个月之间蔓延的平均速度等于在第 到第
到第 个月之间蔓延的平均速度.
个月之间蔓延的平均速度.
其中正确的说法有 .(请把正确说法的序号都填在横线上)
某单位为了了解用电量 度与气温
度与气温
 之间的关系,随机统计了某
之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表
天的用电量与当天气温,并制作了对照表

由表中数据得回归直线方程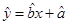 中
中 ,预测当气温为
,预测当气温为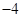
 时,用电量的度数是 .
时,用电量的度数是 .
某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
t |
70 |
根据上表求出y关于x的线性回归方程为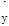 =6.5x+17.5,则表中t的值为_ .
=6.5x+17.5,则表中t的值为_ .
具有线性相关关系的变量x,y,满足一组数据如下表所示:

若y与x的回归直线方程为 ,则m的值是 .
,则m的值是 .
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量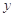 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y= x+1上,则这组样本数据的样本相关系数为 .
x+1上,则这组样本数据的样本相关系数为 .
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
| 时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
| 10:00 |
9.5 |
300 |
| 11:00 |
9.6 |
220 |
注: ,
,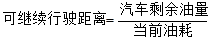 ,
,
 .
.
从以上信息可以推断在10:00—11:00这一小时内 (填上所有正确判断的序号).
行驶了80公里;
行驶不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
平均车速超过80公里/小时.
已知x、y的取值如下表所示,若y与x线性相关,且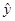 =0.95x+
=0.95x+ ,则
,则 =____________.
=____________.
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法示得回归直线方程为 。
。
零件数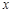 (个) (个) |
10 |
20 |
30 |
40 |
50 |
加工时间 |
62 |
|
75 |
81 |
89 |
表中有一个数据模糊不清,经推断,该数据的值为 .
试题篮
()