高中数学变量间的相关关系填空题

某医疗研究所为了检验某种血清预防感冒的作用，把500名使用血清的人与另外500名未使用血清的人的一年中的感冒记录作比较，提出假设H₀:“这种血清不能起到预防感冒的作用”。对此利用2×2列联表计算得χ²≈3.918,经查对临界值表知P(χ²≥3.841)≈0.05。对此四名同学做出了如下的判断：
①有95%的把握认为“这种血清能起到预防感冒的作用”；②如果某人未使用该血清，那么他在一年中有95%的可能性得感冒；③这种血清预防感冒的有效率为95%；  ④这种血清预防感冒的有效率为5%；
其中判断正确的序号是              。

某医疗研究所为了检验某种血清预防感冒的作用，把名使用血清的人与另外名未用血清的人一年中的感冒记录作比较，提出假设：“这种血清不能起到预防感冒的作用”，利用列联表计算得，经查对临界值表知．对此，四名同学做出了以下的判断：
：有的把握认为“这种血清能起到预防感冒的作用”
：若某人未使用该血清，那么他在一年中有的可能性得感冒
：这种血清预防感冒的有效率为    
：这种血清预防感冒的有效率为 
则下列结论中，正确结论的序号是     
① ；   ②；  ③；  ④

某产品的广告费用x与销售额y的统计数据如下表
根据上表可得回归方程中的为9.4，据此模型预报广告费用为6万元时销售额为          万元。

经统计，某小店卖出的饮料杯数y杯与当天气温x℃的回归方程为
．若天气预报说“明天气温为2℃”，则该小店明天大约可卖出饮料          
杯．

已知的取值如下表所示：

x	0	1	3	4
y	2.2	4.3	4.8	6.7

从散点图分析，与线性相关，且，则_______________

.假设关于某设备的使用年限x和所支出的维修费用 y（万元），有如下的统计资料： 

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7. 0

若由资料可知y对x呈线性相关关系，且线性回归方程为，其中已知，请估计使用年限为20年时，维修费用约为_________.

关于x与y，有如下数据

x	2	4	5	6	8
y	30	40	60	50	70

有如下的两个模型：①＝6.5x＋17.5，②＝7x＋17.通过残差分析发现第①个线性模型比第②个拟合效果好．则R________R，Q₁________Q₂.
(用大于，小于号填空，R，Q分别是相关指数和残差平方和)

给出以下变量①吸烟，②性别，③宗教信仰，④国籍
其中属于分类变量的有________

对具有线性相关关系的变量x和y，测得一组数据如下表：

	3	4	5	6
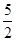		3	4

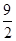若它们的线性回归方程为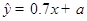，则的值为    

已知x、y之间的一组数据为：x:  0    1     2     3   
y:  1    3     5     7
则y与x的线性回归方程必过点＿

为了判断高中三年级学生选修文科是否与性别有关，现随机抽取50名学生，
得到如下22联表：

	理科	文科
男	13	10
女	7	20

根据表中的数据，则认为选修文科与性别有关出错的可能性为       ．

在对两个变量x,y进行线性回归分析时有以下步骤：
（1）利用回归方程进行预测；
（2）收集数据；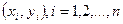
（3)求线性回归方程；
（4）根据所收集的数据绘制散件图.
则正确的操作顺序是____________

对一些城市进行职工人均工资水平x（千元）与居民人均消费水平y（元）统计调查后知，y与x具有相关关系，满足回归方程。若某被调查城市居民人均消费水平为7.675（千元），则可以估计该城市人均消费额占人均工资收入的百分比约为
      %（保留两个有效数字）

已知与之间的部分对应关系如下表：

	11	12	13	14	15	…
						…

则和可能满足的一个关系式是                      ．

对两个具有线性相关关系的变量进行回归分析时，得到一个回归方程为，，则       .