高中数学变量间的相关关系填空题

下表为某公司员工连续加班时间与制造产品的几组数据，根据表中提供的数据，求出y关于的线性回归方程为，则表中t的值为       .

	3	4	5	6
	2.5	t	4	4.5

 

某产品的广告费用x与销售额y的统计数据如表，根据此表可得回归方程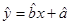中的 为9.4，据此模型预报广告费用为6万元时销售额为                   

广告费用x（万元）	4	2	3	5
销售额y（万元）	49	26	39	54

已知x与y之间的一组数据：

x	0	1	2	3
y	1	3	5	7

则y与x的线性回归方程为y=bx+a必过点__________________________.

对于有线性相关关系的变量x，y，测得一组数据如下表：

x	2	4	5	6	8
y	20	40	60	70	80

根据上表得它们的回归直线方程为，据此模型来预  测当x=20时，y的估计值为                

已知回归直线方程＝0.6x－0.71，则当x＝25时，y的估计值是________．

某种产品的广告费用支出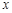与销售额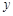之间有如下的对应数据：

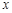	2	4	5	6	8
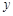	30	40	60	50	70

则回归直线方程为                 

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了 5次试验.根据收集到的数据(如下表），由最小二乘法求得回归方程

现发现表中有一个数据模糊看不清，请你推断出该数据的值为______

某工厂的某种型号的机器的使用年限和所支出的维修费用(万元)有下表的统计资料：

	2	3	4	5	6
	2.2	3.8	5.5	6.5	7.0

 
根据上表可得回归方程，据此模型估计，该型号机器使用年限为10年时维修费用约         万元（结果保留两位小数）．

给出下列命题：
①线性回归方程 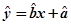必过；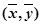
②函数的零点有2个；
③函数的图象与轴围成的图形面积是；
④函数是偶函数，且在区间内单调递增；
⑤函数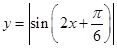的最小正周期为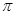.其中真命题的序号是           。

某地区恩格尔系数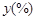与年份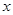的统计数据如下表:

年份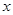	2004	2005	2006	2007
恩格尔系数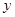(%)	47	45.5	43.5	41

从散点图可以看出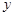与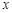线性相关，且可得回归直线方程为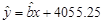，据此模型可预测2013年该地区的恩格尔系数(%)为     ．

已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是________________.

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验.根据 收集到的数据（如下表），由最小二乘法求得回归直线方程

表中有一个数据模糊不清，请你推断出该数据的值为______ .

下表是某厂1～4月份用水量(单位：百吨)的一组数据，

月份x	1	2	3	4
用水量y	4.5	4	3	2.5

 
由其散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是y＝－0.7x＋a，则a＝____   __.

某单位为了了解用电量度与气温℃之间的关系，随机统计了某4天的用电量与当天气温.由表中数据得线性方程中，据此预测当气温为5℃时，用电量的度数约为        。

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．
根据收集到的数据（见下表），由最小二乘法求得回归方程

现发现表中有一个数据模糊看不清，请你推断出该数据的值为               ．