某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
一名小学生的年龄和身高(单位:cm)的数据如下:
年龄 |
6 |
7 |
8 |
9 |
身高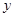 |
118 |
126 |
136 |
144 |
由散点图可知,身高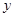 与年龄
与年龄 之间的线性回归直线方程为
之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A.154 B. 153 C.152 D. 151
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验。
(1)求选取的2组数据恰好是相邻两个月的概率;
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线
性回归方程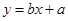 ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
随机变量X的分布列为
| X |
1 |
2 |
4 |
| P |
0.5 |
0.2 |
0.3 |
则E(3X+4)=________.
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且  =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
从某居民区随机抽取10个家庭,获得第 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得 ,
, ,
, ,
, .
.
(1)求家庭的月储蓄 对月收入
对月收入 的线性回归方程
的线性回归方程 ;
;
(2)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为
附:线性回归方程 中,
中, ,
, ,
,
下列说法中正确的是( )
A.若分类变量 和 和 的随机变量 的随机变量 的观测值 的观测值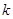 越大,则“ 越大,则“ 与 与 相关”的可信程度越小 相关”的可信程度越小 |
B.对于自变量 和因变量 和因变量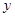 ,当 ,当 取值一定时, 取值一定时,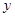 的取值具有一定的随机性, 的取值具有一定的随机性, , ,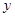 间的这种非确定关系叫做函数关系 间的这种非确定关系叫做函数关系 |
C.相关系数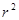 越接近1,表明两个随机变量线性相关性越弱 越接近1,表明两个随机变量线性相关性越弱 |
D.若分类变量 与 与 的随机变量 的随机变量 的观测值 的观测值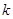 越小,则两个分类变量有关系的把握性越小 越小,则两个分类变量有关系的把握性越小 |
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
某单位为了了解用电量 (千瓦时)与气温
(千瓦时)与气温 (
( )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温 ( ( ) ) |
18 |
13 |
10 |
 |
用电量 (千瓦时) (千瓦时) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程 中
中 ,预测当气温为
,预测当气温为 时,用电量约为( )
时,用电量约为( )
A.58千瓦时 B.66千瓦时 C.68千瓦时 D.70千瓦时
在线性回归模型 中,下列说法正确的是( )
中,下列说法正确的是( )
A. 是一次函数 是一次函数 |
B.因变量 是由自变量 是由自变量 唯一确定的 唯一确定的 |
C.因变量 除了受自变量 除了受自变量 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的产生 的产生 |
D.随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差 的产生 的产生 |
有下列关系:
①人的年龄与他(她)拥有的财富之间的关系;
②曲线上的点与该点的坐标之间的关系;
③苹果的产量与气候之间的关系;
④森林中的同一种树木,其横断面直径与高度之间的关系,
其中有相关关系的是( )
| A.①②③ | B.①② | C.②③ | D.①③④ |
已知变量x,y之间具有线性相关关系,其回归方程为 =-3+bx,若
=-3+bx,若 则b的值为( )
则b的值为( )
| A.2 | B.1 | C.-2 | D.-1 |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,给定下列结论:
=0.85x-85.71,给定下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本点的中心(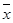 ,
, );
);
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
试题篮
()