为了考察两个变量 和
和 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量 的观测数据的平均值都是,那么下列说法正确的是( )
的观测数据的平均值都是,那么下列说法正确的是( )
A. 和 和 有交点 有交点 |
B. 与 与 相交,但交点不一定是 相交,但交点不一定是 |
C. 与 与 必定平行 必定平行 |
D. 与 与 必定重合 必定重合 |
某种商品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出
(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与
与 的线性回归方程为
的线性回归方程为 ,则表中的
,则表中的 的值为( )
的值为( )
| A.45 | B.50 | C.55 | D.60 |
实验测得四组(x,y)的值分别为(1,2),(2,3),(3,4),(4,4),则y与x间的线性回归方程是( )
| A.y=-1+x | B.y=1+x | C.y=1.5+0.7x | D.y=1+2x |
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| |
喜欢 |
不喜欢 |
合计 |
| 大于40岁 |
20 |
5 |
25 |
| 20岁至40岁 |
10 |
20 |
30 |
| 合计 |
30 |
25 |
55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的2×2列联表:
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由χ2= 算得,
算得,
χ2=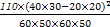 ≈7.8.
≈7.8.
以下结论正确的是( )
(A)有99%以上的把握认为“选择过马路的方式与性别有关”
(B)有99%以上的把握认为“选择过马路的方式与性别无关”
(C)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
(D)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =bx+a.
=bx+a.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.
(1)根据以上数据建立一个2×2的列联表.
(2)有多大的把握认为“喜欢玩电脑游戏与认为作业多有关系”?
(参考数值: ≈5.059)
≈5.059)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
由表中数据算出线性回归方程 =bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a=
=bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a= -b
-b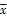 ).
).
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单元:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: =0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
=0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
总计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 总计 |
30 |
20 |
50 |
则在犯错误的概率不超过 的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:χ2=
| P(χ2≥x0) |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| x0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| |
物理 成绩好 |
物理 成绩不好 |
合计 |
| 数学成绩好 |
62 |
23 |
85 |
| 数学成绩不好 |
28 |
22 |
50 |
| 合计 |
90 |
45 |
135 |
那么有把握认为数学成绩与物理成绩之间有关的百分比为( )
(A)25% (B)75% (C)95% (D)99%
关于线性回归,以下说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 |
| B.在平面直角坐标系中用描点的方法得到的表示具有相关关系的两个变量的一组数据的图形叫做散点图 |
C.线性回归直线方程最能代表观测值x,y之间的关系,且其回归直线一定过样本中心点(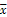 , , ) ) |
| D.甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性作试验,并由回归分析法分别求得相关系数rxy如下表 |
| |
甲 |
乙 |
丙 |
丁 |
| rxy |
0.82 |
0.78 |
0.69 |
0.85 |
则甲同学的试验结果体现A,B两变量更强的线性相关性
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A.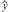 =-10x+200 =-10x+200 |
B.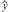 =10x+200 =10x+200 |
C.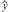 =-10x-200 =-10x-200 |
D.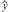 =10x-200 =10x-200 |
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
A. =1.23x+4 =1.23x+4 |
B. =1.23x+5 =1.23x+5 |
C. =1.23x+0.08 =1.23x+0.08 |
D. =0.08x+1.23 =0.08x+1.23 |
试题篮
()