已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程 =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
通过随机询问110名性别不同的人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由K2= ,得K2=
,得K2=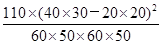 ≈7.8.
≈7.8.
附表:
| P(K2≥k0) |
0.050 |
0.010 |
0.001 |
| k0 |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论 ( ).
A.有99%以上的把握认为“选择过马路的方式与性别有关”
B.有99%以上的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
在2013年3月15日这天,郑州市物价部门对本市5家商场某商品一天的销售量及其价格进行了调查,5家商场某商品的销售价格x(元)与销售量y(件)之间的一组数据如下表:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
作出散点图,可知销售量y与价格x之间具有线性相关关系,其线性回归方程是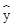 =-3.2x+
=-3.2x+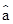 则实数
则实数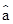 的值是________.
的值是________.
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且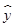 =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
3 |
4 |
5 |
6 |
| 销售额y(万元) |
25 |
30 |
40 |
45 |
根据上表可得回归方程 =
=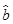 x+
x+ 中的
中的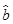 为7.据此模型预报广告费用为10万元时销售额为________(万元).
为7.据此模型预报广告费用为10万元时销售额为________(万元).
为了调查某地居民的年收入x(单位:万元)和年饮食支出y(单位:万元)之间的关系,用分层抽样的方法从该地调查了若干户家庭,调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程为=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出增加________万元.
若回归直线方程的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( ).
A.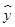 =1.23x+4 =1.23x+4 |
B.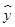 =1.23x+5 =1.23x+5 |
C.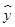 =1.23x+0.08 =1.23x+0.08 |
D.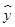 =0.08x+1.23 =0.08x+1.23 |
假设学生在初一和初二数学成绩是线性相关的,若10个学生初一(x)和初二(y)数学分数如下:
| x |
74 |
71 |
72 |
68 |
76 |
73 |
67 |
70 |
65 |
74 |
| y |
76 |
75 |
71 |
70 |
76 |
79 |
65 |
77 |
62 |
72 |
则初一和初二数学分数间的回归方程是 ( ).
A.  =1.218 2x-14.192 B.
=1.218 2x-14.192 B. =14.192x+1.218 2
=14.192x+1.218 2
C.  =1.218 2x+14.192 D.
=1.218 2x+14.192 D.  =14.192x-1.218 2
=14.192x-1.218 2
已知回归直线的斜率的估计值为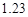 ,样本点的中心为
,样本点的中心为 ,则回归直线方程为
,则回归直线方程为
A.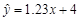 |
B.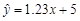 |
C.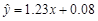 |
D. |
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
A.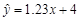 |
B.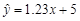 |
C. |
D. |
某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表:据上表可得回归直线方程 =b
=b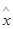 +a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
+a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
| A.48 | B.49 | C.50 | D.51 |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归直线方程 ,表中有一个数据模糊不清,请你推断出该数据的值为( )
,表中有一个数据模糊不清,请你推断出该数据的值为( )
| A.75 | B.62 | C.68 | D.81 |
某城市近10年居民的年收入 与支出
与支出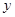 之间的关系大致符合
之间的关系大致符合 (单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
(单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
某城市近10年居民的年收入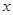 与支出
与支出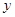 之间的关系大致符合
之间的关系大致符合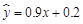 (单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
(单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| |
关注NBA |
不关注NBA |
合计 |
| 男生 |
|
6 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为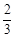 .
.
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
| P(K2≥k) |
0.10 |
0.05 |
0.010 |
0.005 |
| K |
2.706 |
3.841 |
60635 |
7.879 |
(参考公式: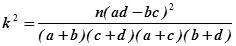 )其中n=a+b+c+d
)其中n=a+b+c+d
试题篮
()