改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) |
1 |
2 |
3 |
4 |
5 |
| 人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有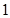 年多于10人的概率.
年多于10人的概率.
(2)根据这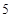 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程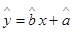 ,并计算第
,并计算第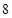 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式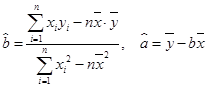
为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
则y对x的线性回归方程为( )
A.y=x-1 B.y=x+1 C.y=88+ x D.y=176
x D.y=176
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 天 天 |
1 |
2 |
3 |
4 |
5 |
被感染的计算机数量 (台) (台) |
10 |
20 |
39 |
81 |
160 |
则下列函数模型中能较好地反映计算机在第 天被感染的数量
天被感染的数量 与
与 之间的关系的是 ( )
之间的关系的是 ( )
A. B.
B. C.
C. D.
D.
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X,若P(X=2)=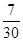 求:
求:
(1)n的值;
(2)X的概率分布与数学期望.
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)画出散点图;
(2)若线性相关,则求出回归方程 ;
;
(3)估计使用年限为10年时,维修费用是多少?
(参考公式: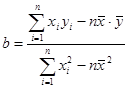 ,
,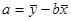 )
)
某种产品的广告费支出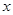 与销售额
与销售额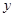 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
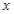 |
2 |
4 |
5 |
6 |
8 |
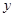 |
30 |
40 |
60 |
50 |
70 |
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:
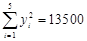
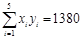
参考公式:线性回归方程系数: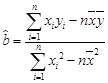 ,
, )
)
某车间加工零件的数量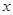 与加工时间
与加工时间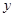 的统计数据如下表:
的统计数据如下表:
现已求得上表数据的回归方程 中的
中的 的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
的值为0.9,则据此回归模型可以预测,加工90个零件所需要的加工时间约为( )
| A.93分钟 | B.94分钟 | C.95分钟 | D.96分钟 |
利用独立性检验来判断两个分类变量X和Y是否有关系,通过查阅下表来确定“X和Y有关系”的可信度.为了调查用电脑时间与视力下降是否有关系,现从某地网民中抽取100位居民进行调查.经过计算得 ,那么就有_______________%的根据认为用电脑时间与视力下降有关系.
,那么就有_______________%的根据认为用电脑时间与视力下降有关系.
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
甲、乙两名同学在 次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为
次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
B. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
D. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
某车间加工零件的数量 与加工时间
与加工时间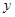 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间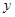 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为 ( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
假设关于某设备的使用年限 和所支出的维修费
和所支出的维修费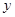 (万元)有如下的统计资料:
(万元)有如下的统计资料:
| 使用年限x |
2 |
3 |
4 |
5 |
6 |
| 维修费用y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
由资料可知y和x呈线性相关关系,由表中数据算出线性回归方程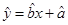 中的
中的 据此估计,使用年限为10年时的维修费用是 万元.
据此估计,使用年限为10年时的维修费用是 万元.
某商品的销售量 (件)与销售价格
(件)与销售价格 (元/件)存在线性相关关系,根据一组样本数据
(元/件)存在线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为 则下列结论正确的是( )
则下列结论正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.若 表示变量 表示变量 与 与 之间的线性相关系数,则 之间的线性相关系数,则 |
| C.当销售价格为10元时,销售量为100件 |
| D.当销售价格为10元时,销售量为100件左右 |
下列四个命题中,正确的是( )
A.已知 服从正态分布 服从正态分布 ,且 ,且 ,则 ,则 |
B.已知命题 ;命题 ;命题 .则命题“ .则命题“ ”是假命题 ”是假命题 |
C.设回归直线方程为 ,当变量 ,当变量 增加一个单位时, 增加一个单位时, 平均增加2个单位 平均增加2个单位 |
D.已知直线 , , ,则 ,则 的充要条件是 的充要条件是 =-3 =-3 |
试题篮
()