给出施化肥量（kg）对水稻产量（kg）影响的试验数据：
| 施化肥量x |
15 |
20 |
25 |
30 |
| 水稻产量y |
330 |
345 |
365 |
405 |
（1）试求出回归直线方程；
（2）请估计当施化肥量为10时，水稻产量为多少？
（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125）
下列结论：①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法．其中正确的是 ．（将所有正确的序号填上）
某服装商场为了了解毛衣的月销售量
(件)与月平均气温
(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：
月平均气温 |
17 |
13 |
8 |
2 |
| 月销售量（件） |
24 |
33 |
40 |
55 |
（1）做出散点图；
(2) 求线性回归方程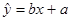
；
(3)气象部门预测下个月的平均气温约为6ºC，据此估计该商场下个月毛衣的销售量．（ 
,
）
对变量x, y 有观测数据（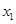
，
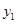）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（
，
）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断。 
图1 图2
| A．变量x 与y 正相关，u 与v 正相关 |
| B．变量x 与y 正相关，u 与v 负相关 |
| C．变量x 与y 负相关，u 与v 正相关 |
| D．变量x 与y 负相关，u 与v 负相关 |
一名小学生的年龄和身高（单位：cm)的数据如下：
| 年龄X |
6 |
7 |
8 |
9 |
| 身高Y |
118 |
126 |
136 |
144 |
由散点图可知，身高y与年龄x之间的线性回归直线方程为
，预测该学生10岁时的身高为( )
A． 154 B． 153 C． 152 D． 151
一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：
| 转速x(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y（件） |
11 |
9 |
8 |
5 |
画出散点图，并通过散点图确定变量y对x是否线性相关；
（2）如果y对x有线性相关关系，求回归直线方程；
（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？(精确到0.0001)
两个变量x，y与其线性相关系数r有下列说法
（1）若r>0，则x增大时，y也相应增大；
（2）若r<0，则x增大时，y也相应增大；
（3）若r＝1或r＝－1，则x与y的关系完全对应(有函数关系)，在散点图上各个散点均在一条直线上，其中正确的有 （ ）
| A．①② | B．②③ | C．①③ | D．①②③ |
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是
.
(Ⅰ)请将上面的列表补充完整（在答题卡上直接填写结果，不需要写求解过程），并据此资料分析反感“中国式过马路 ”与性别是否有关？（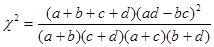
当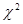
<2.706时,没有充分的证据判定变量性别有关，当
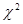>2.706时,有90％的把握判定变量性别有关，当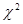>3.841时,有95％的把握判定变量性别有关，当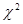>6.635时,有99％的把握判定变量性别有关）
(Ⅱ）若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望.
某车间加工零件的数量
与加工时间
的统计数据如下表：
| 零件数（个） |
10 |
20 |
30 |
| 加工时间（分钟） |
21 |
30 |
39 |
现已求得上表数据的回归方程
中的
值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为 （ ）
A．84分钟 B．94分钟 C．102分钟 D．112分钟
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
| A．y＝－10x＋200 | B．y＝10x＋200 |
| C．y＝－10x－200 | D．y＝10x－200 |
已知一个线性回归方程为
＝2x＋45，其中x的取值依次为1, 7, 5, 13, 19，
则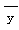
＝ ( )
| A．58.5 | B．46.5 | C．63 | D．75 |
为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
５０ |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
．
（1）请将上面的列联表补充完整；
（2）是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关？说明你的理由.下面的临界值表供参考：
 |
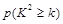0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005] |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式：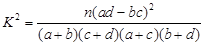
，其中
)
工人月工资y（元）与劳动生产率x（千元）变化的回归方程
，下列判断正确的是 ( )
①劳动生产率为1千元时，工资约为130元
②劳动生产率提高1千元时，月工资约提高80元
③劳动生产率提高1千元时，月工资约提高130元
④当月工资为210元时，劳动生产率约为2千元
| A．① ② | B．① ② ④ | C．② ④ | D．① ② ③ ④ |
已知
、
之间的一组数据如右表：
|
0 |
1 |
2 |
3 |
|
8 |
2 |
6 |
4 |
则线性回归方程
所表示的直线必经过点 ( )
A．（0，0） B．（1.5,5） C．（4,1.5） D．（2,2）
试题篮
()
粤公网安备 44130202000953号
=
，其中
样本中心点为（1,2 ）则回归直线方程为（ ）
