变量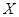 与
与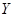 相对应的一组数据为
相对应的一组数据为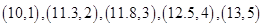 ,变量
,变量 与
与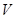 相对应的一组数据为
相对应的一组数据为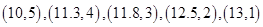 .
.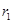 表示变量
表示变量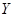 与
与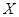 之间的线性相关系数,
之间的线性相关系数,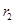 表示变量
表示变量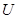 与
与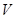 之间的线性相关系数,则( )
之间的线性相关系数,则( )
A.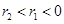 |
B.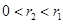 |
C.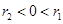 |
D. |
经过长期的观测得到:在交通繁忙的时段内,蚌埠市解放路某路段汽车的车流量 (千辆/h)与汽车的平均速度
(千辆/h)与汽车的平均速度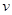 (
( )之间的函数关系为
)之间的函数关系为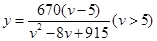 。
。
(1)在该时段内,当汽车的平均速度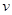 为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
为多少时车流量最大,最大车流量为多少?(精确到0.1千辆/h)
(2)若要求在该时段内车流量超过10千辆/h,则汽车的平均速度应在什么范围内?
根据如下样本数据得到的回归方程为 ,则
,则
 |
3 |
4 |
5 |
6 |
7 |
8 |
 |
 |
 |
 |
 |
 |
 |
A. ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,
(本小题满分18分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温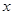 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量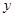 (杯),得到如下数据:
(杯),得到如下数据:
| 日 期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温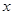 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量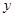 (杯) (杯) |
23[] |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程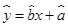 .
.
(参考公式: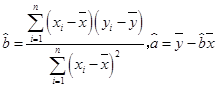 .)
.)
已知x,y取值如表:
| x |
0 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.0 |
9.3 |
9.1 |
从所得的散点图分析可知,y与x线性相关,且y=0.95x+a,则a=( )
A.1.30 B.1.45 C.1.65 D.1.80
在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:

参照附表,下列结论正确的是( ).
A.在犯错误的概率不超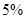 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; |
B.在犯错误的概率不超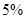 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; |
C.有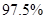 的把握认为“小动物是否被感染与有没有服用疫苗有关”; 的把握认为“小动物是否被感染与有没有服用疫苗有关”; |
D.有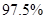 的把握认为“小动物是否被感染与有没有服用疫苗无关”. 的把握认为“小动物是否被感染与有没有服用疫苗无关”. |
已知具有线性相关的两个变量x,y之间的一组数据如下:
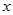 |
0 |
1 |
2 |
3 |
4 |
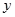 |
2.2 |
4.3 |
t |
4.8 |
6.7 |
且回归方程是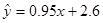 ,则t=( )
,则t=( )
A.2.5 B.3.5 C.4.5 D.5.5
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间
与时间 间的关系为
间的关系为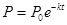 .若在前5个小时消除了
.若在前5个小时消除了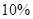 的污染物,则污染物减少
的污染物,则污染物减少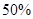 所需要的时间约为( )小时.(已知
所需要的时间约为( )小时.(已知 =0.3010,
=0.3010,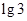 =0.4771)
=0.4771)
| A.26 | B.33 | C.36 | D.42 |
登山族为了了解某山高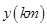 与气温
与气温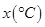 之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(°C) |
18 |
13 |
10 |
-1 |
| 山高y(km) |
24 |
34 |
38 |
64 |
由表中数据,得到线性回归方程
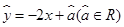 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8 C.-4 D.-6
为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
| 父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
| 儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
则y对x的线性回归方程为( )
A.y = x-1 B.y = x+1 C.y =" 88+"  D.y = 176
D.y = 176
已知具有线性相关关系的变量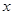 和
和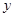 ,测得一组数据如下表:若已求得它们的回归直线方程的斜率为6.5,则这条回归直线的方程为 .
,测得一组数据如下表:若已求得它们的回归直线方程的斜率为6.5,则这条回归直线的方程为 .
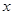 |
2 |
4 |
5 |
6 |
8 |
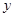 |
10 |
20 |
40 |
30 |
50 |
某商店对每天进店人数 与某种商品成交量
与某种商品成交量 (单位:件)进行了统计,得到如下对应数据:
(单位:件)进行了统计,得到如下对应数据:
 |
 |
 |
 |
 |
 |
 |
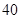 |
 |
 |
 |
 |
 |
 |
 |
 |
由表中数据,得线性回归方程为 .如果某天进店人数是
.如果某天进店人数是 人,预测这一天该商品销售的件数为( )
人,预测这一天该商品销售的件数为( )
A. B.
B. C.
C. D.
D.
试题篮
()