某食品的保鲜时间
(单位:小时)与储藏温度
(单位:
)满足函数关系
(
为自然对数的底数,
为常数).若该食品在
的保鲜时间是
小时,在
的保鲜时间是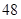 小时,则该食品在
的保鲜时间是()
小时,则该食品在
的保鲜时间是()
| A. | 16小时 | B. | 20小时 | C. | 24小时 | D. | 21小时 |
某食品的保鲜时间 (单位:小时)与储存温度 (单位: )满足函数关系 ( 为自然对数的底数, 为常数).若该食品在 的保鲜时间设计192小时,在 的保鲜时间是48小时,则该食品在的 保鲜时间是小时.
已知变量和
满足关系
,变量
与
正相关. 下列结论中正确的是()
| A. |
|
| B. |
|
| C. |
|
| D. |
|
为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
| 收入
(万元) |
8.2 |
8.6 |
10.0 |
11.3 |
11.9 |
| 支出
(万元) |
6.2 |
7.5 |
8.0 |
8.5 |
9.8 |
根据上表可得回归直线方程
,其中
,据此估计,该社区一户收入为15万元家庭年支出为( )
| A. |
11.4万元 |
B. |
11.8万元 |
C. |
12.0万元 |
D. |
12.2万元 |
在下列各量之间,存在相关关系的是 ( )
①正方体的体积与棱长之间的关系; ②一块农田的水稻产量与施肥量之间的关系;
③人的身高与年龄之间的关系; ④家庭的支出与收入之间的关系;
⑤某户家庭用电量与电价之间的关系。
| A.②③ | B.③④ | C.④⑤ | D.②③④ |
十字路口车流量被定义为单位时间内通过十字路口的车辆数,小张上班经过的某十字路口某时间段内车流量变化近似符合函数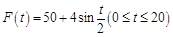 (
(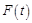 的单位是辆/分,
的单位是辆/分,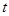 的单位是分),则下列时间段内车流量增加的是
的单位是分),则下列时间段内车流量增加的是
A.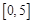 |
B.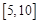 |
C.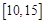 |
D.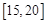 |
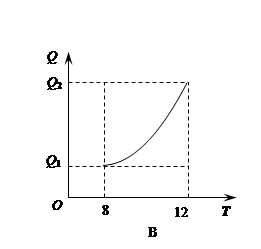
水厂监控某一地区居民用水情况,该地区A,B,C,D四个小区在8:00—12:00时用水总量Q与时间t的函数关系如图所示,在这四个小区中,单位时间内用水量逐步增加的是( )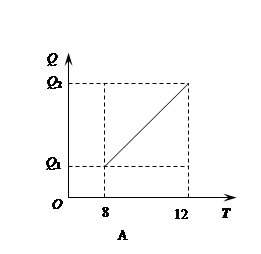


给出下列四个结论:
①若 组数据
组数据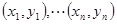 的散点都在
的散点都在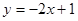 上,则相关系数
上,则相关系数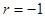 ;
;
②由直线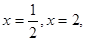 曲线
曲线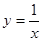 及
及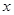 轴围成的图形的面积是
轴围成的图形的面积是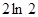 ;
;
③已知随机变量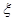 服从正态分布
服从正态分布
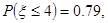 则
则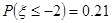 ;
;
④设回归直线方程为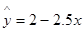 ,当变量
,当变量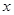 增加一个单位时,
增加一个单位时, 平均增加2个单位.
平均增加2个单位.
其中正确结论的个数为
A.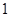 |
B.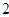 |
C.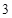 |
D.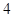 |
以下四个命题中
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②对于命题 :
: 使得
使得 . 则
. 则
 :
: 均有
均有 ;
;
③设随机变量  ,若
,若 ,则
,则 ;
;
④两个随机变量的线性相关性越强,则相关系数就越接近于1.
其中真命题的个数为[来
| A.1 | B.2 | C.3 | D.4 |
下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
| 身高 |
170 |
171 |
166 |
178 |
160 |
| 体重 |
75 |
80 |
70 |
85 |
65 |
若两个量间的回归直线方程为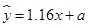 ,则身高为185cm的学生的体重约为( )
,则身高为185cm的学生的体重约为( )
A.87.6kg B.89.5kg C.91.4kg D.92.3kg
试题篮
()