根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：
| 降水量X |
 |
 |
 |
 |
工期延误天数 |
0 |
2 |
6 |
10 |
历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0．3，0．7，0．9．求：
（1）工期延误天数的均值与方差；（2）在降水量X至少是300的条件下，工期延误不超过6天的概率．
以下四个命题中：
①为了了解800名学生对学校某项教改试验的意见，打算从中抽取一个容量为
的样本，考虑用系统抽样，则分段的间隔
为40.
②线性回归直线方程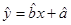
恒过样本中心
，且至少过一个样本点；
③在某项测量中，测量结果ξ服从正态分布
．若ξ在
内取值的概率为
，则ξ在
内取值的概率为
；
其中真命题的个数为（ ）
A． |
B． |
C． |
D． |
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天
名网友的网购金额情况，得到如下数据统计表（如图）：
若网购金额超过
千元的顾客定义为“网购达人”，网购金额不超过千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为
．
（1）试确定
，
，
，
的值，并补全频率分布直方图（如图(2)）．
（2）该营销部门为了进一步了解这
名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定
人，若需从这人中随机选取
人进行问卷调查．设
为选取的人中“网购达人”的人数，求的分布列和数学期望．
假设某市今年高考考生成绩
服从正态分布
，现有2500名考生，据往年录取率可推测今年约有1000名高考考生考上一类大学，估计今年一类大学的录取分数线为 分．（其中
）
试题篮
()
粤公网安备 44130202000953号
服从正态分布
，则
（ ）
（
,
）的图象如图
所示,则（ ）
,
,
,
服从正态分布，其密度函数为
密度曲线如右图，已知该校学生总数是10000人,则成绩位于
的人数约是 .
服从标准正态分布N（0,1），已知
等于
服从正态分布
，若
，则
的值为
服从正态分布
，若
，则
.