已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( )
| A.0.2 | B.0.3 | C.0.4 | D.0.6 |
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:

(I)求这500件产品质量指标值的样本平均值和样本方差
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标服从正态分布
 ,其中
,其中近似为样本平均数
,
 近似为样本方差
近似为样本方差.
(i)利用该正态分布,求;
(ii)某用户从该企业购买了100件这种产品,记表示这100件产品中质量指标值位于区间
的产品件数.利用(i)的结果,求
.
附:
若 则
则 ,
, 。
。
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X |
 |
 |
 |
 |
工期延误天数 |
0 |
2 |
6 |
10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.求:
(1)工期延误天数 的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)= .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):

若网购金额超过 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为 .
.
(1)试确定 ,
, ,
, ,
, 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)).
(2)该营销部门为了进一步了解这 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查.设
人进行问卷调查.设 为选取的
为选取的 人中“网购达人”的人数,求
人中“网购达人”的人数,求 的分布列和数学期望.
的分布列和数学期望.
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布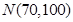 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(1)、试问此次参赛学生总数约为多少人?
(2)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可供查阅的(部分)标准正态分布表
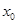 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
.某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走,第一条路线穿过
市区,路线较短,但交通拥挤,所需时间(单位为分)服从正态分布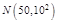 ;第二条
;第二条
路线沿环城公路走,路程较长,但交通阻塞少,所需时间服从正态分布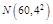 .
.
(1)若只有70分钟可用,问应走哪条路线?
(2)若只有65分钟可用,又应走哪条路线
据调查统计,某市高二学生中男生的身高X(单位:cm)服从正态分布N(174,9),若该市共有高二男生3 000人,试计算该市高二男生身高在(174,180]范围内的人数.
设不等式x2+y2£ 4确定的平面区域为U,ïxï+ïyï£ 1确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(2)在区域U内任取3个点,记这3个点在区域V的个数为X,求X的分布列和数学期望EX.
在函数 ,
, 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明.
生产工艺工程中产品的尺寸偏差 ,如果产品的尺寸与现实的尺寸偏差的绝对值不超过4mm的为合格品,求生产5件产品的合格率不小于
,如果产品的尺寸与现实的尺寸偏差的绝对值不超过4mm的为合格品,求生产5件产品的合格率不小于 的概率.(精确到0.001).
的概率.(精确到0.001).
试题篮
()