因为指数函数 是增函数(大前提),而
是增函数(大前提),而 是指数函数(小前提),所以
是指数函数(小前提),所以 是增函数(结论)”,上面推理的错误是 ( )
是增函数(结论)”,上面推理的错误是 ( )
| A.大前提错导致结论错 | B.小前提错导致结论错 |
| C.推理形式错导致结论错 | D.大前提和小前提都错导致结论错 |
“所有金属都能导电,铁是金属,所以铁能导电”这种推理属于( ).
| A.演绎推理 | B.类比推理 | C.合情推理 | D.归纳推理 |
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1) 求出 ,
,

 并猜测
并猜测 的表达式;
的表达式;
(2) 求证: +
+ +
+ +…+
+…+
 .
.
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
. . . . .
按照以上排列的规律,第n行( )从左向右的第3个数为
)从左向右的第3个数为
德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是指分子为 ,分母为正整数的分数),称为莱布尼兹三角形:
,分母为正整数的分数),称为莱布尼兹三角形:
根据前5行的规律,写出第6行的数依次是 
古希腊著名的毕达哥拉斯学派把 ,这样的数称为“三角形数”,而把1,4,9,
,这样的数称为“三角形数”,而把1,4,9, 这样的数称为“正方形数”.如图可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 (填序号)
这样的数称为“正方形数”.如图可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 (填序号)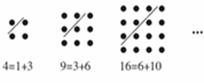
①13=3+10; ②25=9+16;
③36=15+21; ④49=18+31;
⑤64="28+36"
用三段论推理命题:“任何实数的平方大于0,因为 是实数,所以
是实数,所以 ,你认为这个推理 ( )
,你认为这个推理 ( )
| A.是正确的 | B.大前题错误 | C.小前题错误 | D.推理形式错误 |
下面几种推理是合情推理的是( )
(1)由圆的性质类比出球的有关性质;
(2)由直角三角形、等腰三角形、等边三角形的内角和是 ,归纳出所有三角形的内角和是
,归纳出所有三角形的内角和是 ;
;
(3)教室内有一把椅子坏了,则该教室内的所有椅子都坏了;
(4)三角形内角和是 ,四边形内角和是
,四边形内角和是 ,五边形内角和是
,五边形内角和是 ,由此得出凸多边形内角和是
,由此得出凸多边形内角和是 .
.
| A.(1)(2) | B.(1)(3)(4) | C.(1)(2)(4) | D.(2)(4) |
试题篮
()