下列推理过程是演绎推理的是
| A.由平面三角形的性质推测空间三棱锥的性质 |
| B.某校高二1班有55人,2班有52人,由此得高二所有班人数都超过50人 |
C.两条直线平行,同位角相等;若 与 与 是两条平行直线的同位角,则 是两条平行直线的同位角,则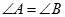 |
D.在数列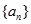 中, 中, , ,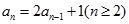 ,由此归纳出 ,由此归纳出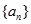 的通项公式 的通项公式 |
下列推理是归纳推理的是( )
A.由于 满足 满足 对 对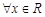 都成立,推断 都成立,推断 为奇函数 为奇函数 |
B.由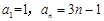 ,求出 ,求出 ,猜出数列 ,猜出数列 的前 的前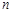 项和的表达式 项和的表达式 |
C.由圆 的面积 的面积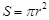 ,推断:椭圆 ,推断:椭圆 的面积 的面积 |
| D.由平面三角形的性质推测空间四面体的性质 |
将正整数从1开始依次写下来,直至2015为止,得到一个新的正整数:1234···201320142015.这个正整数是几位数 ( )
| A.3506位数 | B.4518位数 | C.6953位数 | D.7045位数 |
有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;直线 ∥平面
∥平面 ,直线
,直线 ;则直线
;则直线 ∥直线
∥直线 ”的结论是错误的原因是: ( )
”的结论是错误的原因是: ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛.顶层一个,以下各层堆成正六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共有 13个花盆,则底层的花盆的个数是( )
| A.91 | B.127 | C.169 | D.255 |
如图是“推理与证明”的知识结构图,如果要加入“归纳”,则应该放在()
| A.“合情推理”的下位 | B.“演绎推理”的下位 |
| C.“直接证明”的下位 | D.“间接证明”的下位 |
由直线与圆相切时,圆心到切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是 ( )
| A.归纳推理 | B.演绎推理 | C.类比推理 | D.传递性推理 |
设 是由任意
是由任意 个人组成的集合,如果
个人组成的集合,如果 中任意4个人当中都至少有1个人认识
中任意4个人当中都至少有1个人认识
其余3个人,那么,下面的判断中正确的是 ( )
A. 中没有人认识 中没有人认识 中所有的人 中所有的人 |
B. 中至多有2人认识 中至多有2人认识 中所有的人 中所有的人 |
C. 中至多有2人不认识 中至多有2人不认识 中所有的人 中所有的人 |
D. 中至少有1人认识 中至少有1人认识 中的所有人 中的所有人 |
下面几种推理中是演绎推理的为
| A.由金、银、铜、铁可导电,猜想:金属都可导电; |
B.猜想数列 的通项公式为 的通项公式为  ; ; |
C.半径为 圆的面积 圆的面积 ,则单位圆的面积 ,则单位圆的面积 ; ; |
D.由平面直角坐标系中圆的方程为 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为 |
老师带甲乙丙丁四名学生去参加自主招生考试,考试结束后老师向四名学生了解考试情况,
四名学生回答如下:
甲说:“我们四人都没考好”;
乙说:“我们四人中有人考的好”;
丙说:“乙和丁至少有一人没考好”;
丁说:“我没考好”.
结果,四名学生中有两人说对了,则四名学生中 两人说对了.( )
| A.甲 丙 | B.乙 丁 | C.丙 丁 | D.乙 丙 |
观察下面关于循环小数化分数的等式: ,据此推测循环小数,
,据此推测循环小数, 可化成分数()
可化成分数()
A.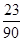 |
B.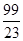 |
C. |
D.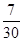 |
试题篮
()