由“在平面内三角形的内切圆的圆心到三边的距离相等”联想到“在空间中内切于三棱锥的球的球心到三棱锥四个面的距离相等”这一推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.联想推理 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线:已知直线 ,直线
,直线 ,直线b∥平面α,则b∥a”的结论显然是错误的,这是因为
,直线b∥平面α,则b∥a”的结论显然是错误的,这是因为
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
下列正确的是( )
| A.类比推理是由特殊到一般的推理 |
| B.演绎推理是由特殊到一般的推理 |
| C.归纳推理是由个别到一般的推理 |
| D.合情推理可以作为证明的步骤 |
下列推理错误的是( )
A.A∈l,A∈α,B∈l,B∈α⇒l α α |
| B.A∈α,A∈β,B∈α,B∈β⇒α∩β=AB |
C.l α,A∈l⇒A∉α α,A∈l⇒A∉α |
D.A∈l,l α⇒A∈α α⇒A∈α |
有一段“三段论”推理是这样的:
因为指数函数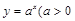 且
且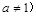 在
在 上是增函数,
上是增函数, 是指数函数,所以
是指数函数,所以 在
在 上是增函数.以上推理中 ( )
上是增函数.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
“指数函数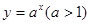 是增函数,
是增函数, 是指数函数,所以
是指数函数,所以 是增函数”,在以上演绎推理中,下列说法正确的是
是增函数”,在以上演绎推理中,下列说法正确的是
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
设 是由任意
是由任意 个人组成的集合,如果
个人组成的集合,如果 中任意4个人当中都至少有1个人认识
中任意4个人当中都至少有1个人认识
其余3个人,那么,下面的判断中正确的是 ( )
A. 中没有人认识 中没有人认识 中所有的人 中所有的人 |
B. 中至多有2人认识 中至多有2人认识 中所有的人 中所有的人 |
C. 中至多有2人不认识 中至多有2人不认识 中所有的人 中所有的人 |
D. 中至少有1人认识 中至少有1人认识 中的所有人 中的所有人 |
下面几种推理中是演绎推理的为
| A.由金、银、铜、铁可导电,猜想:金属都可导电; |
B.猜想数列 的通项公式为 的通项公式为  ; ; |
C.半径为 圆的面积 圆的面积 ,则单位圆的面积 ,则单位圆的面积 ; ; |
D.由平面直角坐标系中圆的方程为 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为 |
老师带甲乙丙丁四名学生去参加自主招生考试,考试结束后老师向四名学生了解考试情况,
四名学生回答如下:
甲说:“我们四人都没考好”;
乙说:“我们四人中有人考的好”;
丙说:“乙和丁至少有一人没考好”;
丁说:“我没考好”.
结果,四名学生中有两人说对了,则四名学生中 两人说对了.( )
| A.甲 丙 | B.乙 丁 | C.丙 丁 | D.乙 丙 |
观察下面关于循环小数化分数的等式: ,据此推测循环小数,
,据此推测循环小数, 可化成分数()
可化成分数()
A.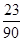 |
B.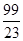 |
C. |
D.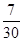 |
我们知道,在边长为a的正三角形内任一点到三边的距离之和为定值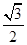 a,类比上述结论,在边长为a的正四面体内任一点到其四个面的距离之和为定值( )
a,类比上述结论,在边长为a的正四面体内任一点到其四个面的距离之和为定值( )
A.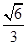 a a |
B.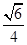 a a |
C. a a |
D.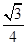 a a |
试题篮
()