高中数学合情推理和演绎推理填空题

观察下列等式
    
   由以上等式推测到一个一般的结论：
对于                                       

平面上，如果△ABC的内切圆半径为r ,三边长分别为，则三角形面积.根据类比推理，在空间中，如果四面体内切球的半径为R，其四个面的面积分别为,则四面体的体积V=_     __.

下图是实数系的结构图,图中1,2,3三个方格中的内容依次为                .
 

已知整数对的序列如下：
(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),
(2,4),…则第60个数对是______________

若数列{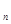}，(n∈N)是等差数列,则有数列b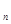=(n∈N)也是等差数列，类比上述性质，相应地：若数列{c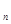}是等比数列,且c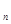＞0(n∈N),则有d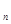="____________" (n∈N)也是等比数列。

若点在内，则有结论 ，把命题类比推广到空间，若点在四面体内，则有结论：              

设，试通过计算来猜想的
解析式：_________________________．

从从1=1，1－4=－(1+2)，1－4+9=1+2+3，1－4+9－16=－(1+2+3+4)，…，推广到第n个等式为                 。

将侧棱相互垂直的三棱锥称为“直角三棱锥”，三棱锥的侧面和底面分别叫为直角三棱锥的“直角面和斜面”；过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”．请仿照直角三角形以下性质：（1）斜边的中线长等于斜边边长的一半；（2）两条直角边边长的平方和等于斜边边长的平方；（3）斜边与两条直角边所成角的余弦平方和等于1．写出直角三棱锥相应性质（至少一条）：_____________________．

已知整数对排列如下，则第60个整数对是_______________.

已知：空间四边形ABCD中，E，F分别为BC，CD的中点，判断直线EF与平面ABD的关系是    .

观察数列:得其中的值依次是____________．

已知：△ABC中，AD⊥BC于D,三边分别是a，b，c，则有；类比上述结论，写出下列条件下的结论：四面体P-ABC中，△ABC，△PAB，△PBC，△PCA的面积分别是，二面角的度数分别是，则                                     ；

在数列中，，，则                ；

已知：△ABC中，AD⊥BC于D,三边分别是a，b，c，则有；类比上述结论，写出下列条件下的结论：四面体P-ABC中，△ABC，△PAB，△PBC，△PCA的面积分别是，二面角的度数分别是，则                                      ；