在△ABC中,若D为BC 的中点,则有 ,将此结论类比到四面体中,在四面体 A-BCD中,若G为△BCD的重心,则可得一个类比结论: .
,将此结论类比到四面体中,在四面体 A-BCD中,若G为△BCD的重心,则可得一个类比结论: .
设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.
其中能推出:“a,b中至少有一个大于1”的条件是______.(填序号)
我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点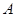
 ,且法向量为
,且法向量为 的直线(点法式)方程为
的直线(点法式)方程为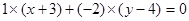 ,化简得
,化简得 .类比以上方法,在空间直角坐标系中,经过点
.类比以上方法,在空间直角坐标系中,经过点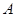
 ,且法向量为
,且法向量为 的平面(点法式)方程为 .
的平面(点法式)方程为 .
如图,在等腰直角三角形 中,斜边
中,斜边 ,过点
,过点 作
作 的垂线,垂足为
的垂线,垂足为 ;过点
;过点 作
作 的垂线,垂足为
的垂线,垂足为 ;过点
;过点 作
作 的垂线,垂足为
的垂线,垂足为 ;…,以此类推,设
;…,以此类推,设 ,
, ,
, ,…,
,…, ,则
,则 ________.
________.
求“方程 的解”有如下解题思路:设
的解”有如下解题思路:设 ,则
,则 在
在 上单调递减,且
上单调递减,且 ,所以原方程有唯一解
,所以原方程有唯一解 .类比上述解题思路,方程
.类比上述解题思路,方程 的解为 .
的解为 .
将演绎推理“函数 的图像是一条直线.”恢复成完全的三段论形式,其中大前提是 .
的图像是一条直线.”恢复成完全的三段论形式,其中大前提是 .
计算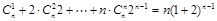 ,可以采用以下方法:
,可以采用以下方法:
构造恒等式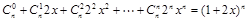 ,
,
两边对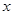 求导,得
求导,得 ,
,
在上式中令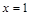 ,得
,得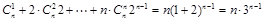 ,
,
类比上述计算方法,计算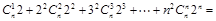 .
.
半径为r的圆的面积 ,周长
,周长 ,若将r看作(0,+∞)上的变量,则
,若将r看作(0,+∞)上的变量,则 ①,①式用语言可以叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为
①,①式用语言可以叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为 的球,若将
的球,若将 看作
看作 上的变量,请写出类比①的等式:____________________.上式用语言可以叙述为_________________________.
上的变量,请写出类比①的等式:____________________.上式用语言可以叙述为_________________________.
记集合T = {0,1,2,3,4,5,6},
 ,将M中的元素按从大到小的顺序排成数列{bi},并将bi按如下规则标在平面直角坐标系的格点(横、纵坐标均为整数的点)处:点(1,0)处标b1,点(1,
,将M中的元素按从大到小的顺序排成数列{bi},并将bi按如下规则标在平面直角坐标系的格点(横、纵坐标均为整数的点)处:点(1,0)处标b1,点(1, )处标b2,点(0,
)处标b2,点(0, )处标b3,点
)处标b3,点 处标b4,点(
处标b4,点( ,0)标b5,点(
,0)标b5,点( ,1)处标b6,点(0,1)处标b7,…,以此类推.
,1)处标b6,点(0,1)处标b7,…,以此类推.
(Ⅰ)标b50处的格点坐标为 ;
(Ⅱ)b50 = .
有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖.有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”.四位歌手的话只有两句是对的,则获奖的歌手是 .
试题篮
()