有一段“三段论”推理是这样的:
因为指数函数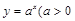 且
且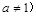 在
在 上是增函数,
上是增函数, 是指数函数,所以
是指数函数,所以 在
在 上是增函数.以上推理中 ( )
上是增函数.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
平面几何中,有边长为 的正三角形内任一点到三边距离之和为定值
的正三角形内任一点到三边距离之和为定值 ,类比上述命题,棱长为
,类比上述命题,棱长为 的正四面体内任一点到四个面的距离之和为 ( )
的正四面体内任一点到四个面的距离之和为 ( )
A. |
B. |
C. |
D. |
有一段“三段论”推理是这样的:
对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点,
的极值点,
因为函数 在
在 处的导数值
处的导数值 ,
,
所以, 是函数
是函数 的极值点.
的极值点.
以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是
| A.2日和5日 | B.5日和6日 |
| C.6日和11日 | D.2日和11日 |
计算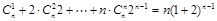 ,可以采用以下方法:
,可以采用以下方法:
构造恒等式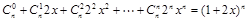 ,
,
两边对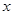 求导,得
求导,得 ,
,
在上式中令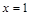 ,得
,得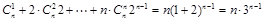 ,
,
类比上述计算方法,计算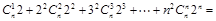 .
.
半径为r的圆的面积S(r)= r2,周长C(r)=2
r2,周长C(r)=2 r,若将r看作(0,+∞)上的变量,则(
r,若将r看作(0,+∞)上的变量,则( r2)’=2
r2)’=2 r ;对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于上述的式子:_______________________.
r ;对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于上述的式子:_______________________.
半径为r的圆的面积 ,周长
,周长 ,若将r看作(0,+∞)上的变量,则
,若将r看作(0,+∞)上的变量,则 ①,①式用语言可以叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为
①,①式用语言可以叙述为:圆的面积函数的导数等于圆的周长函数.对于半径为 的球,若将
的球,若将 看作
看作 上的变量,请写出类比①的等式:____________________.上式用语言可以叙述为_________________________.
上的变量,请写出类比①的等式:____________________.上式用语言可以叙述为_________________________.
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
A.当 时,该命题不成立 时,该命题不成立 |
B.当 时,该命题成立 时,该命题成立 |
C.当 时,该命题成立 时,该命题成立 |
D.当 时,该命题不成立 时,该命题不成立 |
有一段“三段论”推理是这样的:
对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点,因为函数
的极值点,因为函数 在
在 处的导数值
处的导数值 ,所以,
,所以, 是函数
是函数 的极值点.以上推理中( )
的极值点.以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令 表示第
表示第 秒时机器人所在位置的坐标,且记
秒时机器人所在位置的坐标,且记 ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A. |
B. |
C. |
D. |
试题篮
()