在 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为______________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为______________________.
有四张卡片,每张卡片有两个面,一个面写有一个数字,另一个面写有一个英文字母.现规定:当卡片的一面为字母 时,它的另一面必须是数字
时,它的另一面必须是数字 .如图,下面的四张卡片的一个面分别写有
.如图,下面的四张卡片的一个面分别写有 ,为检验此四张卡片是否有违反规定的写法,则必须翻看的牌是( )
,为检验此四张卡片是否有违反规定的写法,则必须翻看的牌是( )
| A.第一张,第三张 | B.第一张,第四张 |
| C.第二张,第四张 | D.第二张,第三张 |
有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖.有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”.四位歌手的话只有两句是对的,则获奖的歌手是 .
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= 根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
设函数f(x)=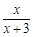 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)=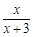 , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))=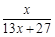 , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))=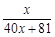 ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:(Ⅰ) 是数列
是数列 中的第_________项;(Ⅱ)若
中的第_________项;(Ⅱ)若 为正偶数,则
为正偶数,则 =_________.(用n表示)
=_________.(用n表示)
试题篮
()