高中数学空间向量的应用试题

如图，矩形中，，为边的中点，将沿直线翻折成，若为线段的中点，则在翻折过程中，下面四个命题中不正确的是（   ）

A．是定值

B．点在某个球面上运动

C．存在某个位置，使

D．存在某位置，使平面

三棱锥中，，，，若，，是该三棱锥外部（不含表面）的一点，则下列命题正确的是（   ）
① 存在无数个点，使；
② 存在唯一点，使四面体为正三棱锥；
③ 存在无数个点，使；
④ 存在唯一点，使四面体有三个面为直角三角形．

A．①③

B．①④

C．①③④

D．①②④

设，，是三个互不重合的平面，，是直线，给出下列命题：①，，则；②若，，，则；③若，在内的射影互相垂直，则；④若，，，则，其中正确命题的个数为（ ）

A．0

B．1

C．2

D．3

如图，AB为圆O的直径，点E、F在圆O上，且AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=AF=1．

（1）求四棱锥F﹣ABCD的体积V_F﹣ABCD；
（2）求证：平面AFC⊥平面CBF；
（3）在线段CF上是否存在一点M，使得OM∥平面ADF，并说明理由．

如图，三棱柱的三视图，主视图和侧视图是全等的矩形，俯视图是等腰直角三角形，点M是A₁B₁的中点．

（1）求证：B₁C//平面AC₁M；
（2）求证：平面AC₁M⊥平面AA₁B₁B．

等边三角形的边长为3，点分别是边上的点，且满足（如图1）．将沿DE折起到的位置，使二面角为直二面角，连结、（如图2）．

（1）求证：平面；
（2）在线段上是否存在点，使直线与平面所成的角为60°？若存在，求出PB的长；若不存在，请说明理由．

在正方体上任意选择4个顶点，由这4个顶点可能构成如下几何体：
①有三个面为全等的等腰直角三角形，有一个面为等边三角形的四面体；
②每个面都是等边三角形的四面体；
③每个面都是直角三角形的四面体；
④有三个面为不全等的直角三角形，有一个面为等边三角形的四面体．
以上结论其中正确的是________(写出所有正确结论的编号)．

设，是两条不同的直线，，是两个不同的平面，则下列命题中正确的是（   ）

A．若，且，则

B．若，且，则

C．若，且，则

D．若，且，则

如图，四棱锥中，底面为矩形，平面，为的中点．

（1）证明：平面；
（2）设，，三棱锥的体积，求到平面的距离．

已知，表示两条不同直线，表示平面．下列说法正确的是（ ）

A．若，，则

B．若，，则

C．若，，则

D．若，，则

如图，已知四棱锥的底面是正方形，侧棱底面．

（1）若，是的中点．证明：平面；
（2）若二面角的余弦值为，试求的值．

如图，在四棱锥中，底面为菱形且，为中点．

（1）若，求证：平面平面；
（2）若，且四棱锥的体积为1，试求二面角的大小．

如图所示，已知空间四边形的每条边和对角线长都等于1，点，，分别是、、的中点，计算：

（1）；
（2）的长；
（3）异面直线与所成角的余弦值．

如图所示，为正方体，给出以下五个结论：

①平面；
②平面；
③与底面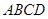所成角的正切值是；
④二面角的正切值是；
⑤过点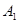且与异面直线和均成角的直线有2条．
其中，所有正确结论的序号为_______．

，是直线上的两点，，于，于，，且直线与直线成的角，则、两点间的距离是_______．