如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( )

| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
已知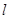 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , ,则 ,则 |
若曲线 的一条切线
的一条切线 与直线x+4y-8=0垂直,则
与直线x+4y-8=0垂直,则 的方程为( )
的方程为( )
| A.4x-y-3=0 | B.x+4y-5=0 |
| C.4x-y+3=0 | D.x+4y+3=0 |
试题篮
()