高中数学误差估计试题

对某同学的6次物理测试成绩（满分100分）进行统计，作出的茎叶图如图所示，给出关于该
同学物理成绩的以下说法：

①中位数为84；②众数为85；③平均数为85；④极差为12；
其中，正确说法的序号是____________．

我县某中学为了配备高一新生中寄宿生的用品，招生前随机抽取部分准高一学生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．

（1）求直方图中的值；
（2）如果上学路上所需时间不少于40分钟的学生应寄宿，且该校计划招生1800名，请估计新生中
应有多少名学生寄宿；
（3）若不安排寄宿的话，请估计所有学生上学的平均耗时（用组中值代替各组数据的平均值）．

下图是某校高二年级举办的歌咏比赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的方差为      ．

下表是一个容量为60的样本（60名学生的数学考试成绩，成绩为0-100的整数）的频率分布表，则表中频率a的值为      ．

分组	0．5～20．5	20．5～40．5	40．5～60．5	60．5～80．5	80．5～100．5
频数	3	6	12
频率				a	0．3

 

若根据10名儿童的年龄 x（岁）和体重 y（㎏）数据用最小二乘法得到用年龄预报体重的回归方程是 y =" 2" x + 7 ，已知这10名儿童的年龄分别是 2、3、3、5、2、6、7、3、4、5，则这10名儿童的平均体重是（ ）

A．17 ㎏

B．16 ㎏

C．15 ㎏

D．14㎏

已知样本9，10，11，x，y的平均数是10，方差是2，则xy=          ．

如图是某电视台综艺节目举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（   ）

A．84；

B．84；

C．85；4

D．85；

200辆汽车通过某一段公路时，时速的频率分布直方图如图所示，则时速在[50，70)的汽车大约有（  ）．

A．60辆

B．80辆

C．70辆

D．140辆

从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表
如下：

分组（重量）
频数（个）	5	10	20	15

（1）根据频数分布表计算苹果的重量在的频率；
（2）用分层抽样的方法从重量在和的苹果中共抽取4个，其中重量在的有几个？
（3）在（2）中抽出的4个苹果中，任取2个，求重量在和中各有1个的概率．

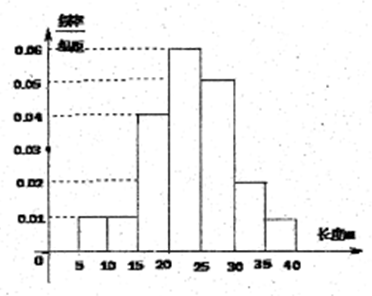
某棉纺厂为了了解一批棉花的质量，从中随机抽取了100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间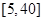中，其频率分布直方图如图所示，则其抽样的100根中，有    根在棉花纤维的长度大于25mm．

从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下．观察图形，回答下列问题：

（1）49．5——69．5这一组的频率和频数分别为多少?
（2）估计这次环保知识竞赛成绩的中位数及平均成绩．（精确到小数点后一位）

孝感市2014年各月的平均气温（）数据的茎叶图如下：
            
则这组数据的中位数是

A．23

B．21．5

C．20

D．19

孝感市2014年各月的平均气温（）数据的茎叶图如下：

则这组数据的中位数是

A．19

B．20

C．21．5

D．23

一组数据的平均数是2．8，方差是3．6，若将这组数据中的每一个数据都加上60，得 到一组新的数据，则所得的新数据的平均数和方差分别是__________．

已知x、y之间的一组数据如下：则线性回归方程所表示的直线必经过点

x	0	1	2	3
y	8	2	6	4

 
A．（1．5，5）        B．（5，1．5）          C．（2，5）          D．（1．5，4）